Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 86b
Para os vetores desenhados na Figura , b) determine o módulo e a direção do produto vetorial
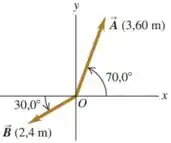
Passo 1
E aí, galerinha!
Nesse problema queremos determinar o modulo e a direção do produto vetorial onde e são dados por
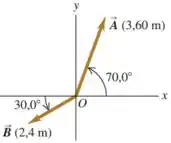
Como é um produto vetorial, sabemos que o vetor resultante vai ser perpendicular aos vetores e ao mesmo tempo. Então a direção dele só pode ser a direção do eixo .
Então o que falta pra nós é saber o módulo desse produto.
Pra isso vamos usar a equação 1.22 do livro:
Onde é o ângulo entre os vetores
Veja só!
Passo 2
O ângulo entre igual a soma de todos os ângulos entre eles, então:
Como e , podemos usar a equação 1.22:
E encontramos a resposta! \O/
Entendeu tudo? Responde Aí!
Resposta
na direção do eixo .
Exercícios de Livros Relacionados
O vetor d 1 → , é paralelo ao semieixo y negativo e o vetor d 2 → é paralelo ao semieixo x positivo. Determine a orientação (a) de d 2 → 4 e (b) de - d 1 → 4 Determine o módulo (c) de d 1 → ⋅ d 2
Um vetor a → de módulo 10 unidades e outro vetor b → de módulo 6,0 unidades fazem um ângulo de 60 ° . Determine (a) o produto escalar dos dois vetores e (b) o módulo do produto vetorial a → × b →
Os vetores a → e b → estão no plano x y . a → tem módulo 8,00 e ângulo 130 ° ; b → tem componentes b x = - 7,72 e b y = - 9,20 . Determine o ângulo entre o semieixo y negativo e (a) o vetor a → ,
Os vetores A → e B → estão no plano x y . A → tem módulo 8,00 e ângulo 130°, B → tem componentes B x = - 7,72 e B y = - 9,20 . (a) Detrmine 5 A → ⋅ B → . Determine 4 A → × 3 B → (b) em termos dos veto
São dados três vetores em metros: d 1 → =- 3 i → +3 j → + 2 k → d 2 → =- 2 i → -4 j → + 2 k → d 3 → =2 i → +3 j → + 1 k → Determine : ( a )d 1 → . d 2 → + d 3 → (b) d 1 → d 2 → xd 3 → (c) d 1 →x( d 2