Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 2.3 - Ex. 15
2.15 Uma tartaruga se arrasta em linha reta, à qual chamaremos de eixo com a direção positiva para a direita. A equação para a posição da tartaruga em função do tempo é .
a) Determine a velocidade inicial, a posição inicial e a aceleração inicial da tartaruga.
b) Em qual instante a velocidade da tartaruga é zero?
c) Quanto tempo do ponto inicial a tartaruga leva para retornar ao ponto de partida? d) Em qual instante t a tartaruga está a uma distância de cm do ponto inicial?
d)Qual é a velocidade (módulo e direção) da tartaruga em cada um desses instantes?
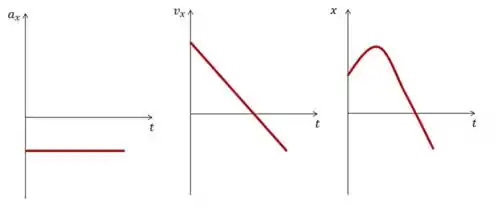
e) Desenhe um gráfico de versus , versus e versus , para o intervalo de tempo até .
Passo 1
Oi, galerinha! Tudo bom? Essa questãozinha é grande, mas nada que assuste a gente, bora lá!!!
Temos uma tartaruguinha andando em linha reta de acordo com a seguinte função:
E quer na letra (a) ele quer saber a velocidade inicial e a aceleração inicial.
Pera que essa fórmula do enunciado lembra do querido “sorvetão”:
Onde, temos que
E só ver que na função, quem acompanha “” é a velocidade inicial e quem acompanha “” é a metade da aceleração inicial.
Bora pra próxima, meu povo!!!
Passo 2
Pra fazer o ítem b) quer saber em qual instante a velocidade da tartaruga é zero, então temos que usar a nossa fórmula para a velocidade:
Lembrando que no Passo 1, vimos que . Substituindo,
Então o tempo é 16 segundos, meus amigos!!
Bora pra letra c)!!
Passo 3
Na letra c), ele pergunta quanto tempo do ponto inicial a tartaruga leva para retornar ao ponto de partida.
Então nessa vamos aplicar o nosso “sorvetão”, mas agora com igual a , que é o ponto inicial, logo:
Temos duas soluções aqui. Tem o , e também tem:
Nesse caso o tempo é igual a segundos, pois significa que ela foi e voltou.
Bora pra próxima!!!
Passo 4
Na letra d) a tartaruga está a do ponto inicial, que é . Ou seja, ela está a ou a !!!!
Agora é só usar nosso “sorvetão” de novo ahaha, mas com .
Realizando a fórmula de Báskara, encontramos ou .
Agora com temos:
Dessa vez temos, porque não existe tempo negativo ahaha.
A velocidade dela nesses instantes vai ser:
1º) :
2º) :
3º) :
Passo 5
e) Desenhe um gráfico de versus t, versus e versus , para o intervalo de tempo até .
Primeiro, vamos pensar na aceleração. Ao longo de todo o tempo, ela mantém um valor constante igual a .
Já a velocidade começa em, ou seja, no início é positiva, mas depois, como a aceleração é negativa, a velocidade vai diminuindo, então o gráfico dela vai ser uma reta decrescente.
Já a posição em função do tempo é descrita por essa equação:
Que é a uma função do segundo grau, ou seja, o gráfico é uma parábola, como a aceleração é negativa, temos que a concavidade é voltada para baixo.
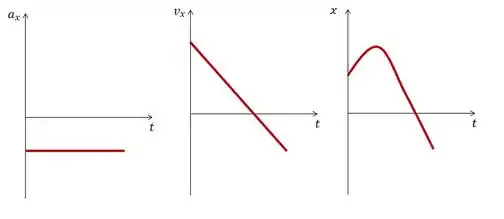
Resposta
a)
b)
c)
d)
e)
