Por meio de desenhos simples dos produtos vetoriais apropriados, demonstre que

a) pode ser interpretado como o produto do módulo de vezes o componente de em relação a , ou o módulo de vezes o componente de em relação a ;

Quando e são perpendiculares , , como na figura:

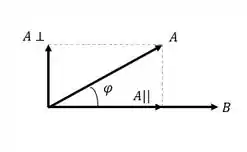
Sabemos que e

não tem componentes em e não tem componentes , e:

Para os vetores paralelos temos que:

E

Assim,

E aí! entendeu tudo? Responde Aí! 😬