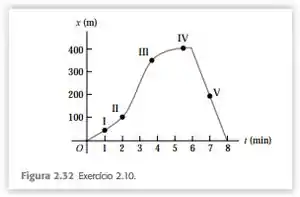
2.10 Uma professora de física sai de sua casa e se dirige a pé para o campus. Depois de 5 min começa a chover e ela retorna para casa. Sua distância da casa em função do tempo é indicada pelo gráfico da Figura 2.32. Em qual dos pontos indicados sua velocidade é: a) zero? b) constante e positiva? c) constante e negativa? d) crescente em módulo? e) decrescente em módulo?
Passo 1
Opa, bora resolver esse problema! Aqui temos um gráfico da distância percorrida em função do tempo:
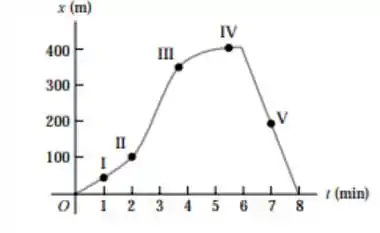
Ele representa uma professora de física sai de sua casa e se dirige a pé para o campus. Depois de 5 min começa a chover e ela retorna para casa.
Sabendo temos que responder várias perguntas sobre a velocidade que ela anda!
Começando pela letra a), que pergunta quando sua velocidade é igual a zero!
A velocidade vai ser 0 quando o tempo passar ela não sair do lugar, ou seja, quando não varia, e esse ponto é o ponto !
Passo 2
Agora na letra b), A velocidade vai ser constante e positiva quando o gráfico mostrar uma linha reta que está subindo, porque se a velocidade não varia, ela não vai produzir curvas no gráfico rsrs. Esse ponto é o ponto I, meus pimpolhos!
Passo 3
Letra c), agora, pedindo o ponto em que é constante e negativa. É só olhar uma linha reta de novo, só que dessa vez ela tem que estar descendo. Esse ponto é o ponto V 😊.
Passo 4
Agora, na letra d), ele quer uma velocidade crescente em módulo. Isso quer dizer que o valor da velocidade tem que estar aumentando, como se ela estivesse acelerando. Pra isso a gente tem que achar o ponto onde o gráfico estava constante ou descendo mas quando passa por ele, faz uma curva pra cima. Esse ponto é o ponto II.
Passo 5
Agora, na letra e), ele quer uma velocidade decrescente em módulo. Isso quer dizer que o valor da velocidade tem que estar diminuindo, como se ela estivesse freando. Pra isso a gente tem que achar o ponto onde o gráfico estava subindo mas quando passar por ele, para de subir. Esse ponto é o ponto III.
E finalizamos a questão 😊.
Resposta
- IV
- I
- V
- II
- III