Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 30.Exercício - Ex. 22
22- Na Figura , a chave é fechada, enquanto a chave é mantida aberta. A indutância é e a resistência é .
Quando a corrente atinge seu valor final, a energia armazenada no indutor é igual a . Qual é a fem da bateria?
Depois que a corrente atinge seu valor final, a chave é aberta e a chave é fechada; quanto tempo é necessário para que a energia armazenada no indutor diminua até , a metade do valor inicial?
Passo 1
Só para ficar claro a Figura na qual a questão se refere é essa aqui:
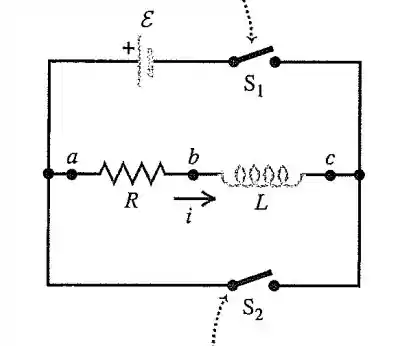
E para resolver a letra nós devemos saber que a energia no indutor vale:
Então a corrente que passa por ele é de:
E essa corrente é a corrente máxima que a bateria pode fornecer, portanto o valor da fem da bateria será:
Uma baita duma bateria, digassi de passagi!
Passo 2
Supondo que o fio onde está a chave está aterrado fazendo com que o indutor passe a descarregar e a chave pare de fornecer energia . Isso faz com que a equação da corrente que passa no indutor seja de descarregamento e seja de:
O que deixa o cálculo da energia no indutor da seguinte maneira:
Então:
O que nos dá um tempo de:
Substituindo os valores de e de nós teremos: