77- Uma barra metálica de comprimento , massa e resistência total está sobre trilhos metálicos sem atrito, inclinados em um ângulo em relação a horizontal. Os trilhos possuem resistência desprezível. Um campo magnético uniforme de módulo está orientado para baixo, como indicado na Figura . A barra é libertada a partir do repouso e desliza para baixo sobre os trilhos.

O sentido da corrente induzida é de para ou de para ?

Qual é a velocidade terminal da barra?

Qual será a corrente induzida na barra quando a velocidade terminal for atingida?

Depois que a velocidade terminal é atingida, qual é a taxa da conversão de energia elétrica em energia térmica na barra?

Depois que a velocidade terminal é atingida, qual é a taxa do trabalho realizado pela força da gravidade? Compare sua resposta a taxa encontrada no item

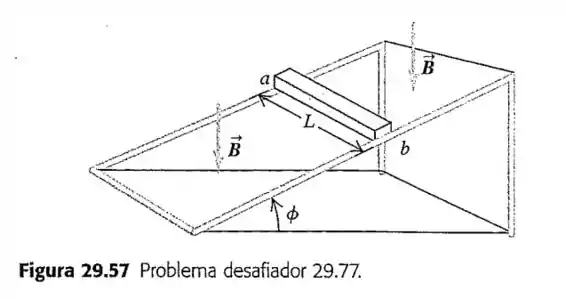
Respondendo a letra , a medida que a barra se desloca para baixo ele se afasta da fonte de campo magnético e pela Lei de Lenz vemos que a barra quer esse campo entrando na barra da mesma forma como entrava antes, forçando um campo magnético induzido que entra nela, portanto pra fazer isso a corrente induzida deverá ser de para .

Essa corrente (causada pelo contato com os trilhos no plano inclinado) gera uma força magnética apontando contra o peso que atua no deslizamento da barra tal como pode se ver abaixo.

De tal forma que a força resultante atua no lado de então:

E a força magnética será igual a:

O termo é por conta da orientação da barra de , para eles estarem perpendiculares nós devemos inclinar a barra um ângulo para cima (a barra está no mesmo sentido de na figura abaixo).

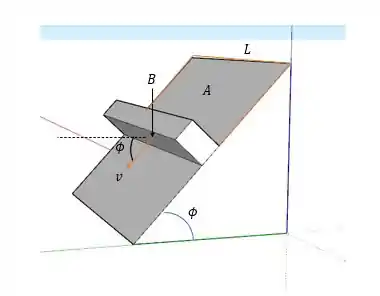
Logo:

Onde a corrente na barra será igual a:

Essa variação de área é o quanto a barra anda no plano inclinado ou seja

Pois a área que precisamos saber é a área que faz com a horizontal.

Então , logo:

Portanto para termos a velocidade de terminal devemos fazer , então: