Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 30.Exercício - Ex. 21

21- Uma bateria de 35.0   V com resistência interna desprezível, um resistor de 50.0   Ω e um indutor de 1.25   m H com resistência interna desprezível estão conectados em série a uma chave aberta. A chave é subitamente fechada

( a ) Quanto tempo após a chave ser fechada a corrente através do indutor atingirá metade do seu valor máximo?

( b ) Quanto tempo após o fechamento da chave a energia armazenada no indutor atingirá a metade do seu valor máximo?

Passo 1

É um circuito R L em série e que pode ser vista no circuito desenhado abaixo:

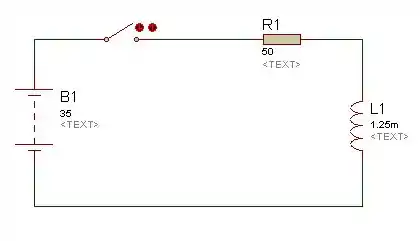
E cuja somatória de tensões (quando fecha-se a chave) pode ser entendida como:

ϵ = R i + L d i d t

O que é uma E D O de primeira ordem cuja variação da corrente pode ser escrita por:

d i d t = ϵ L   e - R L t

E o valor máximo de corrente ocorro quando t = ∞ e d i d t = 0 e será quando nenhuma ‘’resistência’’ é oferecida pelo indutor, ou seja quando

i = ϵ R = 35 50 = 0.7   A

Então queremos saber o tempo necessário para quando a corrente é de 0.35   A , i = ϵ 2 R ou seja:

d i = ϵ L   e - R L t   d t

Integrando os dois lados de 0 até t nós temos.

i = ϵ R 1 - e - R t L

Isolando t nessa equação nós teremos:

1 - R i ϵ = e - R t L

Tirando ln dos dois lados:

ln ⁡ 1 - R i ϵ = - R t L

t = - L R ln ⁡ 1 - R i ϵ

Onde i = ϵ 2 R então:

t = - L R ln ⁡ 1 2

Substituindo os valores de L e de R nós teremos:

t = - 1.25 × 10 - 3 50 ln ⁡ 1 2 = 17.33 μ s

Passo 2

A energia acumulada em um indutor pode ser calculada como:

U = 1 2 L i 2

E a máxima energia é conseguida quando temos a corrente máxima ou seja:

U = 1 2 L ϵ R 2

Então a metade da energia máxima será em:

1 4 L ϵ R 2 = 1 2 L ϵ R 1 - e - R t L 2

Pois i em qualquer momento será dado pela equação

i = ϵ R 1 - e - R t L

Então, cortando todas as partes iguais.

1 2 = 1 - e - R t L 2

1 2 = 1 - e - R t L

e - R t L = 1 - 1 2 = 2 - 1 2

Tirando l n nos dois lados teremos:

- R t L = ln ⁡ 2 - 1 2

t = - L R   ln ⁡ 2 - 1 2

Substituindo os valores de L e de R teremos:

t = - 1.25 × 10 - 3 50   ln ⁡ 2 - 1 2 = 30.7   μ s

Resposta

a )   t = 17.33   μ s

b )   t = 30.7   μ s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Partindo da equação 30.9 , deduza com detalhes a equação 30.11 para a densidade de energia de um toróide preenchido com um material magnético.
Existe uma proposta para usar grandes indutores como dispositivos para armazenar energia. a Qual é a energia total convertida em energia térmica e energia luminosa quando uma lâmpada incandescente de
Um resistor de 15,0 Ω e uma bobina estão conectados em série a uma bateria de 6.3 V com resistência interna desprezível e uma chave fechada. a Após 2,0m s da abertura da chave, a corrente diminuiu par
Um solenoide toroidal de ar possui 300 espiras e um raio médio de 12,0c m , com seção reta de área igual a 4,0c m 2 . Supondo que a corrente seja de 5.0 A , calcule: a O campo magnético do solenoide.
Um indutor com uma indutância de 2.5 H e uma resistência igual a 8.0Ω está conectado aos terminais de uma bateria com fem de 6.0 V e resistência interna desprezível. Calcule a a taxa inicial do cresci