Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 19.3 - Ex. 24

A 273   K e 1,00.10 - 2   a t m , a massa específica de um gás é 1,24.10 - 5   g / c m 3 . (a) Determine v r m s para as moléculas do gás. (b) Determine a massa molar do gás e (c) Identifique o gás. (Sugestão: O gás aparece na tabela.)

Passo 1

Fala galerinha bonita, show de bolinhas com vocês?

Saca só, vamos dar uma olhada na lei dos gases ideais:

p V = n R T

A massa específica é o seguinte:

ρ = m V

Podemos fazer essas grandezas aparecerem na primeira equação se lembrarmos que o número de mols n é simplesmente a massa m dividida pela massa molar M , então:

p V = m M R T

p = m V R T M

Ou seja:

p = ρ R T M

ρ = p M R T

Passo 2

(a) O enunciado pediu pra calcularmos a velocidade média quadrática de um gás que tem:

ρ = 1,24 × 10 - 5   g/cm³

p = 1,24 × 10 - 2  kg /cm³

Ou seja, um gás em que:

p M R T = 1,24 × 10 - 2

Agora vamos isolar o R T / M , que é quem aparece na fórmula da velocidade média quadrática:

R T M = p 1,24 × 10 - 2

E a pressão foi dada no enunciado, é:

p = 1,00 × 10 - 2   atm

p = 1,0 1 × 10 3   P a

Logo:

R T M = 1,01 × 10 3 1,24 × 10 - 2

R T M = 814542,6129

Como a fórmula da velocidade média quadrática é:

v m s = 3 R T M

v m s = 3 814552,6129

v m s = 494   m/s

Passo 3

(b) Vamos voltar na fórmula que tínhamos encontrado para a massa específica:

ρ = p M R T

Podemos isolar a massa molar aqui:

M = ρ R T p

M = 1,24 × 10 - 2 8,32 273 1,0 1 × 10 3

M = 0,027886   kg/mol

Ou seja:

M = 27,9   g/mol

Passo 4

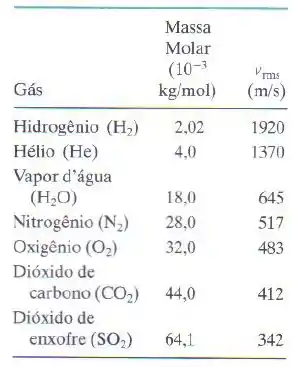
(c) Agora é só a gente olhar a tabela e ver qual gás tem a massa molar mais próxima desse valor:

O N 2 tem massa molar M = 28   g/mol .

Pronto, é ele mesmo.

Resposta

(a) v m s = 494   m/s .

(b) M = 27,9   g/mol .

(c) É o nitrogênio ( N 2 ) .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A velocidade de escape das moléculas de gás na atmosfera de Júpiter é 60k m / s e a temperatura da superfície de Júpiter é tipicamente - 150 graus Celsius. Calculade as velocidades rms para (a) H 2 (b
Podemos usar v r m s = 3 R T M para calcular as velocidades rms de H2, O2 e CO2 a 123 K e depois comparar essas velocidades com 20% da velocidade de escape em Júpiter para decidir a probabilidade de e
Use o cálculo para mostrar que f ( v ) , dada pela Equação 17-36, tem seu valor máximo em uma velocidade v = 2 k T m .
Ache a temperatura na velocidade rms de uma molécula de hidrogênio, quando a mesma é igual a 343m / s .
Dada a integral ∫ 0 ∞ v 3 e - a v 2 d v = 1 2 a 2 , calcule a rapidez media v m é d é das moléculas de um gas usando a função de distrubuição Maxwell-Boltzmann.