Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 38.Exercícios - Ex. 10
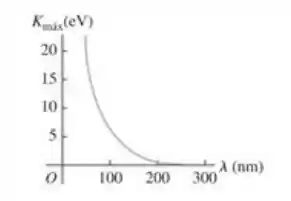
38.10. Em uma experiencia com efeito fotoelétrico, a energia cinética máxima dos fotoelétrons ejetados é medida em vários comprimentos de onda da luz incidente. A figura 38.35 mostra um gráfico dessa energia cinética máxima, , em função do comprimento de onda da luz que incide sobre a superfície do metal. Qual é a) frequência de corte e b) a função trabalho (em eletron-volt) desse metal? c) Dados de experiências como essa muitas vezes são expressos em gráficos mostrando em função de . Faça um esboço qualitativo (sem números) de como pareceria esse gráfico. Identifique o comprimento de onda de corte em seu esboço. Qual é a vantagem de dispor os dados em um gráfico dessa forma?
Passo 1
Bom, a frequência de corte vai acontecer quando a energia cinética máxima for igual a . Olhando no gráfico, a gente consegue ver que isso acontece quando o comprimento de onda é igual a .
Agora que temos o comprimento de onda, podemos calcular a frequência de corte, basta fazer
Então
E essa é a frequência de corte.
Passo 2
Agora vamos para o item (b). Calcular a função trabalho. Para isso podemos usar essa equação
O valor da constante de Planck está no apêndice do livro, e a frequência de corte nós calculamos no passo anterior, então é só substituir os valores, mas o exercício pede a resposta em , então temos que colocar a constante de Planck em
Passo 3
Para produzir o gráfico do item (c) a gente precisa saber o seguinte, é linear em relação a , desde que .
É mais vantajoso usar esse gráfico porque gráficos lineares são mais fáceis de interpretar que gráficos curvilíneos.
