Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 4.Problemas - Ex. 30
Dois corpos são conectados por uma corda leve que passa sobre uma polia sem atrito, como mostrado na Figura P4.30. Considere que a rampa é sem atrito e , e .
- Desenhe diagramas de corpo livre para ambos os corpos. Encontre
- o módulo da aceleração dos corpos,
- a tensão na corda e
- a velocidade de cada corpo depois de de sua liberação do repouso.
Passo 1
E aiii gente, tudo bom com vocês?
Vamos fazer mais uma questão?
Bora comigo!
Letra a:
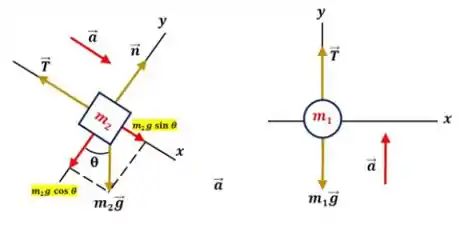
Abaixo temos os diagramas de corpo livre:
Passo 2
Letra b:
Usando a segunda lei de Newton em y:
Usando a segunda lei de Newton em x:
Então, para a:
Passo 3
Letra c:
Passo 4
Letra d:
Resposta
- Ver diagrama
Exercícios de Livros Relacionados
Dois corpos são conectados por uma corda que passa sobre uma polia sem atrito, como na Figura Ativa 4.12a, onde m 1m 2 e a 1 e a 2 são os módulos das respectivas acelerações. Qual enunciado matemático
Um bloco de 15,0l b está no chão. Que força o chão exerce sobre o bloco?Uma corda é amarrada no bloco e passada verticalmente sobre uma polia. A outra extremidade é presa a um corpo de 10,0l b suspens
Uma configuração semelhante à mostrada na Figura P4.20 é frequentemente utilizada em hospitais para sustentar e aplicar uma força de tração horizontal a uma perna machucada. Determine a força de tensã
Dois corpos com massas de 3,00k g e 5,00k g estão ligados por uma corda inextensível que passa sobre uma polia sem atrito para formar uma máquina de Atwood, conforme mostrado na Figura Ativa 4.12a. De
Um corpo de massa m 1=5,00k g colocado sobre uma mesa horizontal sem atrito é conectado a uma corda que passa sobre uma polia e então é presa a um corpo pendurado de massa m 2=9,00k g , como mostrado