Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 4.Problemas - Ex. 18

Dois corpos com massas de 3,00   k g e 5,00   k g estão ligados por uma corda inextensível que passa sobre uma polia sem atrito para formar uma máquina de Atwood, conforme mostrado na Figura Ativa 4.12a. Determine

  1. a tensão na corda,
  2. a aceleração de cada corpo e
  3. a distância que cada corpo se moverá no primeiro segundo de movimento se partirem do repouso.

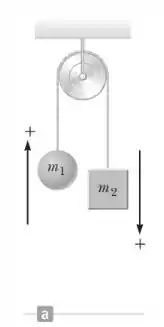
Figura Ativa 4.12a

Passo 1

E aiii gente, tudo bom com vocês?

Vamos fazer uma questãozinha aqui?

Vem comigo e bora!

Primeiro, considere a massa subindo de 3,00 kg. As forças nele são a tensão T, e seu peso, 29.4N. Com a direção para cima como positiva, a segunda lei torna-se:

∑ F y = m a y : T - 29.4 N = 3.00 k g a                       ( 1 )

As forças na massa de 5 kg são seu peso e T, e sua aceleração é a mesma que a da massa que está subindo. Chamando a direção positiva para baixo para esta massa, temos:

∑ F y = m a y : 49 N - T = 5.00 k g a                               2

As equações (1) e (2) podem ser resolvidas simultaneamente, adicionando-as:

T - 29.4 N + 49.0 N - T = 3.00 k g a + 5.00 k g a

Passo 2

Letra b:

Isso nos dá a aceleração de:

a = 19.6 N 8.00 k g = 2.45 m s 2

Então,

T - 29.4 N = 3.00 k g 2.45 m s 2 = 7.35 N

E, portanto, a tensão é T = 36.8 N .

Passo 3

Letra c:

Considere qualquer uma das massas. Nós temos:

y = v i t + 1 2 a t 2 = 0 + 1 2 2.45 m s 2 ( 1.00 s ) 2 = 1.23 m

Resposta

  1. 3.00 k g a + 5.00 k g a
  2. T = 36.8 N .
  3. 1.23 m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

33. O coeficiente de atrito estático entre os dois blocos da FIGURA P7.33 vale 0,60 . O coeficiente de atrito cinético entre o bloco inferior e o piso é de 0,20 . A força F → faz com que os dois bloco
38. O coeficiente de atrito cinético entre o bloco de 2,0k g da FIGURA P7.38 e a mesa vale 0,30 . Quanto vale a aceleração do bloco de 2,0k g ?
36. O bloco de 100k g da FIGURA P7.36 leva 0,6s para chegar ao piso após ser solto a partir do repouso. Qual é a massa do bloco da esquerda?
39. A FIGURA P7.39 mostra um bloco de massa m em repouso sobre uma rampa com 20 ° de inclinação. Os coeficientes de atrito do bloco com a superfície são μ e = 0,80 e μ c = 0,50 . Ele está ligado a out
13 . | Jimmy acaba de pegar dois peixes no Arroio Amarelo. Ele prendeu ao rabo de uma carpa de 1,5k g a linha onde está fisgada uma truta de 3,0k g . A fim de mostrar os peixes a um amigo, ele ergue a