Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 36
36. O bloco de da FIGURA P7.36 leva para chegar ao piso após ser solto a partir do repouso. Qual é a massa do bloco da esquerda?
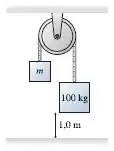
Passo 1
Então pessoal a base que precisamos para resolver esse problema é a segunda e a terceira lei de Newton, mas para sabermos como usá-las bem, vamos montar um diagrama de corpo livre para cada bloco do nosso sistema, temos o seguinte:
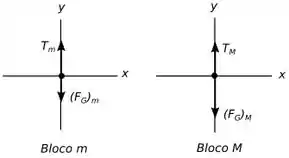
Vamos nos referir ao bloco de massa como bloco e o de massa como bloco .
Agora vamos analisar a nossa situação junto com o diagrama para ver se temos forças iguais presentes.
Dessa situação podemos dizer que a tração em é igual tração em já que eles estão ligados pela mesma corda sem massa passando por uma polia sem massa e sem atrito.
Para encontrarmos a massa de vamos fazer uma análise nas forças dos blocos utilizando a segunda lei de Newton.
Os blocos apresentam uma aceleração já que eles estavam em repouso e essa aceleração vai ser a mesma para os dois blocos com sentido contrário () pelo mesmo argumento da corda não ter massa e não é deformada no movimento.
Mas precisamos achar essa aceleração e para isso vamos usar a cinemática ao nosso favor, usando a seguinte equação:
Já que temos todas as informações do enunciado e da figura, assim é só isolar e calcular seu valor.
Passo 2
Vamos então encontrar a aceleração dos blocos, temos o seguinte:
Substituindo com o que sabemos, temos:
Então temos que:
Passo 3
Agora vamos analisar os dois blocos usando a segunda lei na direção .
Primeiro para , temos:
Agora para o bloco , temos:
Como comentamos no passo temos que , então podemos igualar essas equações, temos:
Agora vamos isolar , temos o seguinte:
Lembrando que , temos:
Substituindo os valores que conhecemos, temos:
Então temos que: