Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 43
43. Os centenários elevadores de Valparaíso, no Chile, são pequenos bondes que sobem e descem as ruas inclinadas. Como mostra a FIGURA P7.43, um elevador sobe enquanto outro desce. Os vagões usam um arranjo de dois cabos para compensar o atrito; um deles passa por uma grande polia e liga os vagões, o segundo é puxado por um pequeno motor. Suponha que a massa de ambos os carros (com seus passageiros) seja de , que o coeficiente de atrito
de rolamento valha e que os vagões se movam com velocidade constante. Quanto vale a tensão no cabo que liga os vagões e no cabo do motor?
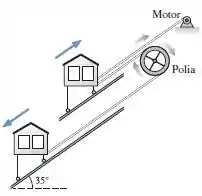
Passo 1
Então pessoal a base que precisamos para resolver esse problema é a segunda e a terceira lei de Newton, mas para sabermos como usá-las bem, vamos montar um diagrama de corpo livre para cada vagão do nosso sistema, temos o seguinte:
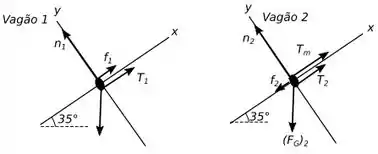
Vamos nos referir ao vagão que está descendo por vagão e o que está subindo de vagão .
Desse diagrama podemos dizer que , já que eles estão presos por uma corda ideal.
Sabendo disso podemos para o item avaliar o vagão utilizando a segunda lei de Newton e encontrar a tensão no cabo que liga os vagões já que as duas são iguais e também porque só teremos a incógnita da tensão.
E para o item podemos avaliar o vagão também utilizando a segunda lei de Newton e encontrar a tração no cabo do motor.
Como os dois vagões estão com velocidade constante isso significa que não temos força resultante na direção e nem na direção .
Passo 2
Vamos lá então, começando com o item vamos analisar o vagão primeiro na direção , temos:
Agora vamos analisar na direção o mesmo vagão, temos:
Usando o que encontramos para , temos:
Isolando que é o que queremos no final das contas.
Substituindo os valores que sabemos, temos:
Passo 3
Agora vamos para o item , para encontrar a tensão no cabo do motor, vamos analisar o vagão .
Primeiro na , que vamos ter uma coisa semelhante ao vagão , temos o seguinte:
Agora vamos analisar a direção , temos:
Usando o que encontramos para , temos:
Isolando , temos:
Como já sabemos , então vamos substituir os valores que conhecemos e encontrar .
Então temos que: