Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 30

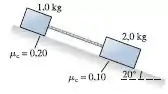
30. Os dois blocos da FIGURA P7.30 escorregam rampa abaixo. Quanto vale a tensão na corda, desprovida de massa?

Passo 1

Então galera para resolver esse problema temos de tomar os eixos x e y de forma diferente, o x paralelo a rampa e o eixo y perpendicular à rampa, assim nosso diagrama de corpo livre fica da seguinte maneira:

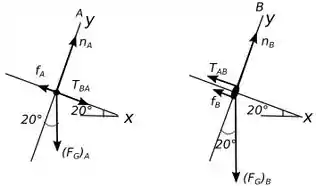
Chamamos o bloco de 1,0   k g de A e o bloco de 2,0   k g de B .

Tendo esse diagrama fica mais fácil de analisar o que temos. Olhe no diagrama que T B A = T A B , já que elas são um par de ação e reação da tração da corda nos blocos.

Para encontrar a tração na corda, que é a mesma que atração nos blocos, logo T B A = T A B = T , vamos usar a segunda lei de Newton na direção x para os dois blocos. A segunda lei nos diz que a soma das forças em uma dada direção é iguala a massa vezes a aceleração.

Passo 2

Vamos então analisar o bloco A , temos o seguinte:

m A a = T B A + F G A sen ⁡ θ - f A

⇒ m A a = T B A + m A g sen ⁡ θ - μ A n A

Como o bloco está em equilíbrio na direção y temos que:

n A = F G A = m A g cos ⁡ θ

Então temos que:

m A a = T B A + m A g sen ⁡ θ - μ A m A g cos ⁡ θ

Passo 3

Vamos então agora analisar o bloco B , temos o seguinte:

m B a = - T A B + F G B sen ⁡ θ - f B

⇒ m B a = - T A B + m B g sen ⁡ θ - μ B n B

Como o bloco está em equilíbrio na direção y temos que:

n B = F G B = m B g cos ⁡ θ

Então temos que:

m B a = - T A B + m B g sen ⁡ θ - μ B m B g cos ⁡ θ

Passo 4

Agora como temos que T B A = T A B = T nossas expressões ficam da seguinte maneira:

m A a = T + m A g sen ⁡ θ - μ A m A g cos ⁡ θ

m B a = - T + m B g sen ⁡ θ - μ B m B g cos ⁡ θ

Se somarmos essas duas equações temos que:

a m A + m B = m A + m B g sen ⁡ θ - ( μ A m A + μ B m B ) g cos ⁡ θ

⇒ a = g sen ⁡ θ - μ A m A + μ B m B g cos ⁡ θ m A + m B

Substituindo os valores que conhecemos, temos:

a = ( 9,8 ) sen ⁡ 20 ° - 0,2 1 + 0,1 2 ( 9,8 ) cos ⁡ 20 ° 1 + 2

= 3,35 - 1,23 3

Então temos que:

a = 2,94   m / s 2

Passo 5

Como sabemos a aceleração podemos pegar qualquer expressão que encontramos e achar o valor de T , eu vou pegar a primeira, mas nada impede de você usar a segunda, assim:

m A a = T + m A g sen ⁡ θ - μ A m A g cos ⁡ θ

Substituindo o que sabemos temos:

( 1 ) ( 2,94 ) = T + ( 1 ) ( 9,8 ) sen ⁡ 20 ° - ( 0,2 ) ( 1 ) ( 9,8 ) cos ⁡ 20 °

2,94 = T + 3,35 - 1,84

Então temos que:

T = 1,43   N

Resposta

T = 1,43   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

20 . || Um cabo de aço maciço arrasta um bloco de 20k g sobre uma superfície horizontal livre de atrito. Uma força de 100N exercida sobre o cabo faz com que o bloco atinja uma velocidade de 4,0m / s a
11 . || Um cabo de aço maciço arrasta um bloco de 20k g sobre uma superfície horizontal sem atrito. Uma força de 100N , exercida sobre o cabo, faz com que o bloco atinja uma velocidade de 4,0m / s ao
24 . || Enquanto dirigia meu carro para o trabalho no ano passado, eu segurava minha caneca de café com a mão esquerda enquanto trocava o CD com a mão direita. Então o celular tocou, de modo que coloq
26 . || Uma espaçonave da Federação ( 2,0 ⋅10 6k g ) usa seu raio-trator para puxar para bordo uma nave de serviço ( 2,0 ⋅10 4k g ) a 10k m de distância. O raio-trator exerce uma força constante de 4,
10 . || Blocos com massas de 1k g , 2k g e3k g são postos em fila, em contato mútuo, sobre uma mesa sem atrito. Os três são empurrados juntos por uma força de 12N exercida sobre o bloco de 1k g . a .