Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 62
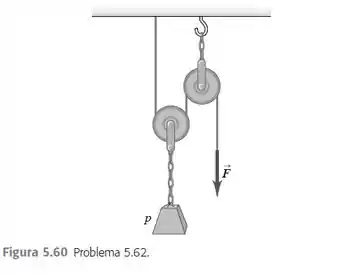
Na Figura 5.60, um trabalhador levanta um peso p puxando uma corda para baixo com uma força . A polia superior está presa ao teto por meio de uma corrente, e a polia inferior está presa ao peso por meio de outra corrente. Ache em termos de p a tensão em cada corrente e o módulo da força , quando o peso é levantado com velocidade constante. Inclua um diagrama do corpo livre ou os diagramas necessários para obter sua resposta. Despreze os pesos das polias, das correntes e da corda.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que um trabalhador levanta um peso puxando uma corda para baixo com uma força com auxílio de algumas polias conforme mostra a figura:
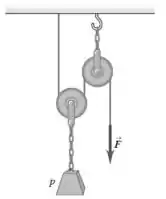
Queremos encontrar a tensão em cada corrente e o módulo da força , quando o peso é levantado com velocidade constante (ou seja, acelera��ão é zero!!).
Para resolver isso, temos que fazer um diagrama de corpo livre do sistema e analisar as forças que estão atuando no corpo.
Também, utilizaremos também a segunda Lei de Newton:
Onde é a força resultante, é a massa e é a aceleração.
Mas antes... vamos interpretar melhor.
Passo 2
Bom... Neste problema, queremos todas as forças atuando nesse sistema em função de , o peso que está sendo levantado pelo trabalhador.
Como a velocidade é constante, a aceleração é zero (). Podemos então considerar que todo o sistema está em equilíbrio.
Então vamos usar essas equações de equilíbrio para achar nossas forcinhas.
Bora desenhar!
Passo 3
Vamos olhar para o peso. Ele tem a corrente que o puxa para cima com força
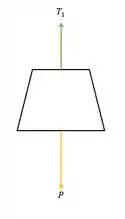
Olhando para o diagrama do peso , temos que
Passo 4
A tensão numa mesma corda é a mesma em todos os pontos. Então, para as polias, nós temos os DCLs:
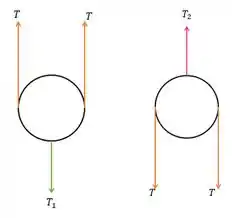
Onde é a tensão na corrente inferior, é a tensão na corrente superior e é a tensão na corda.
Passo 5
Olhando para a polia da esquerda, como tá tudo em equilíbrio, temos que:
Substituindo
Como:
Assim, o módulo da força :
Olhando agora para a polia da direita:
Substituindo :