Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 5.Problemas - Ex. 114

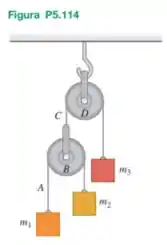
Na Figura P5.114, as massas m 1 e m 2 está conectadas por um fio leve A que passa sobre uma polia leve e sem atrito B. O eixo da polia B é conectado por um segundo fio leve C que passa sobre uma segunda polia leve e sem atrito D a uma massa m 3 . A polia D está fixa ao teto por seu eixo. O sistema é liberado a partir do repouso. Em termos de m 1 , m 2 e m 3 e de g , qual é (a) a aceleração do bloco m 3 ? (b) a aceleração da polia B? (c) A aceleração do bloco m 1 ? (d) A aceleração do bloco m 2 ? (e) A tensão na corda A? (f) A tensão na corda C? (g) O que suas expressões fornecem para m 1 = m 2 e m 3 = m 1 + m 2 ? O resultado era esperado?

Passo 1

Fala galerinha, beleza?

O primeiro passo para resolver esse problema é desenhar as forças que agem sobre cada bloco:

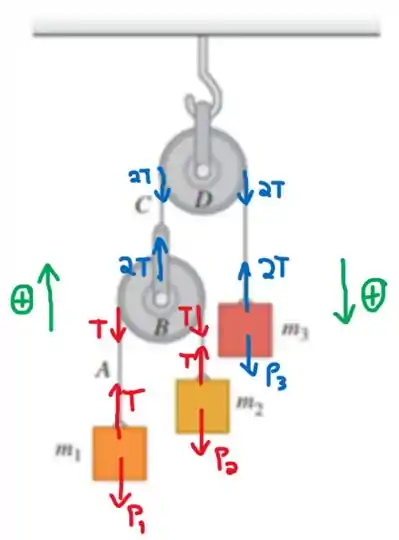
Vale destacar que podemos transmitir as tensões como sendo iguais pelos fios pois eles são ideais (sem massa), assim como as polias. Observe também que eu defini uma convenção de sinal: sinais positivos para o bloco m 3 caindo e os demais subindo. Caso o sinal encontrado seja negativo, o movimento é invertido...

Vamos escrever a segunda lei de Newton para cada bloco:

T - P 1 = m 1 a 1 T - P 2 = m 2 a 2 P 3 - 2 T = m 3 a 3

Note que temos três equações e quatro incógnitas ( a 1 , a 2 , a 3 e T ). Vamos precisar achar alguma relação extra entre as acelerações para resolver o sistema...

Passo 2

É fácil perceber que a aceleração do bloco m 3 é igual a aceleração da polia B:

a 3 = a B

Vamos olhar para o referencial da polia B, como se ela estivesse parada. Nesse contexto, a aceleração do bloco m 2 é - a e do bloco m 1 é + a . Quando passamos para o referencial usual:

a 2 = - a + a B             e             a 1 = a + a B

Somando as duas equações:

a 1 + a 2 = 2 a B → a 1 + a 2 = 2 a 3

Essa era a equação que faltava para montarmos o sistema!

T - P 1 = m 1 a 1 T - P 2 = m 2 a 2 P 3 - 2 T = m 3 a 3 a 1 + a 2 = 2 a 3

Passo 3

Somando as três primeiras equações:

P 3 - P 1 - P 2 = m 1 a 1 + m 2 a 2 + m 3 a 3

No lugar de a 3 substituímos

a 3 = a 1 + a 2 2

Assim,

P 3 - P 1 - P 2 = m 1 a 1 + m 2 a 2 + m 3 a 1 + a 2 2

Da primeira equação, temos que

T = m 1 a 1 + P 1

Da segunda:

T = m 2 a 2 + P 2

Igualando as duas:

m 1 a 1 + P 1 = m 2 a 2 + P 2 → a 2 = m 1 a 1 + P 1 - P 2 m 2

Substituindo isso na relação anterior:

P 3 - P 1 - P 2 = m 1 a 1 + m 1 a 1 + P 1 - P 2 + m 3 2 a 1 + m 1 a 1 + P 1 - P 2 m 2

Ou ainda,

P 3 - 2 P 1 = 2 m 1 a 1 + m 3 2 m 2 a 1 + m 1 a 1 + P 1 - P 2 m 2

Portanto,

P 3 - 2 P 1 = 2 m 1 a 1 + m 3 2 m 2 m 2 a 1 + m 1 a 1 + P 1 - P 2

Multiplicando a equação toda por 2 m 2 :

2 P 3 m 2 - 4 P 1 m 2 = 4 m 1 m 2 a 1 + m 2 m 3 a 1 + m 1 m 3 a 1 + m 3 P 1 - m 3 P 2

Logo,

4 m 1 m 2 + m 2 m 3 + m 1 m 3 a 1 = 2 P 3 m 2 - 4 P 1 m 2 - m 3 P 1 + m 3 P 2

Substituindo P = m g , temos que

4 m 1 m 2 + m 2 m 3 + m 1 m 3 a 1 = 3 m 2 m 3 g - 4 m 1 m 2 g - m 1 m 3 g

Portanto,

a 1 = g 3 m 2 m 3 - 4 m 1 m 2 - m 1 m 3 4 m 1 m 2 + m 2 m 3 + m 1 m 3

Passo 4

Agora que temos a 1 , podemos achar a 2 usando

m 1 a 1 + P 1 = m 2 a 2 + P 2 → m 1 a 1 + g = m 2 a 2 + g

Logo,

a 2 = m 1 m 2 a 1 + g - g

Portanto,

a 2 = m 1 m 2 g 3 m 2 m 3 - 4 m 1 m 2 - m 1 m 3 4 m 1 m 2 + m 2 m 3 + m 1 m 3 + g - g

Logo,

a 2 = m 1 m 2 g 4 m 2 m 3 4 m 1 m 2 + m 2 m 3 + m 1 m 3 - g = g 4 m 1 m 3 4 m 1 m 2 + m 2 m 3 + m 1 m 3 - 1

Assim,

a 2 = g 3 m 1 m 3 - 4 m 1 m 2 - m 2 m 3 4 m 1 m 2 + m 2 m 3 + m 1 m 3

Com isso, podemos tirar a 1 :

a 3 = 1 2 a 1 + a 2 =

Fazendo as contas, achamos

a 3 = a B = g m 2 m 3 - 4 m 1 m 2 + m 1 m 3 4 m 1 m 2 + m 2 m 3 + m 1 m 3

Usando T = m 1 a 1 + P 1 , achamos

T = g 4 m 1 m 2 m 3 4 m 1 m 2 + m 2 m 3 + m 1 m 3

Com isso,

T A = T = g 4 m 1 m 2 m 3 4 m 1 m 2 + m 2 m 3 + m 1 m 3

T C = 2 T = g 8 m 1 m 2 m 3 4 m 1 m 2 + m 2 m 3 + m 1 m 3

Passo 5

Por fim, vamos ao último item! Quando m 1 = m 2 = m e m 3 = m 1 + m 2 = 2 m , obtemos

a 1 = a 2 = a 3 = 0

Repare que isso faz total sentido, já que nesse caso os dois lados se equilibram!

Resposta

a 1 = g 3 m 2 m 3 - 4 m 1 m 2 - m 1 m 3 4 m 1 m 2 + m 2 m 3 + m 1 m 3

a 2 = g 3 m 1 m 3 - 4 m 1 m 2 - m 2 m 3 4 m 1 m 2 + m 2 m 3 + m 1 m 3

a B = a 3 = g m 2 m 3 - 4 m 1 m 2 + m 1 m 3 4 m 1 m 2 + m 2 m 3 + m 1 m 3

T A = g 4 m 1 m 2 m 3 4 m 1 m 2 + m 2 m 3 + m 1 m 3

T C = g 8 m 1 m 2 m 3 4 m 1 m 2 + m 2 m 3 + m 1 m 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Figura 5.60, um trabalhador levanta um peso p puxando uma corda para baixo com uma força F → . A polia superior está presa ao teto por meio de uma corrente, e a polia inferior está presa ao peso po
Determine a força P necessária para suportar  a massa  de  20  kg  usando  a  talha  do  tipo   “Spanish Burton”. Além disso, quais  são  as  reações nos  ganchos de apoio A, B e C?
Determine a  força P necessária para manter a  massa de 50 kg em equilíbrio.
Os princípios de uma talha diferencial são indicados esquematicamente na fi gura. Determine a intensidade da  força P necessária para suportar  força  de 800 N. Além disso, encontre a distância x onde