Exercícios de Polias Móveis - Lista de Exercícios Resolvida
Questão 1
A força da Fig. 12-67 mantém o bloco de e as polias em equilíbrio. As polias têm massa e atrito desprezíveis. Calcule a tensão do cabo de cima.
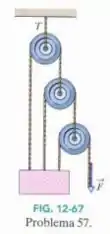
Questão 2
Na figura abaixo tem-se uma massa que está conectada a uma massa através das polias e que tem massas despreziveis. Supondo que a massa desliza sobre a mesa sem atrito e que a aceleração da massa é vertical e para baixo, pede-se:
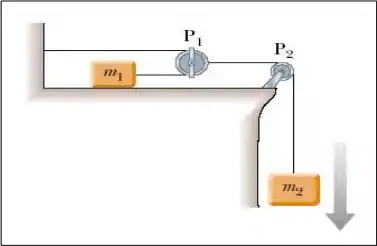
(a) Coloque em um diagrama todas as forças que atuam no sistema.
(b) Determinar o valor numérico da razão , considerando os fios inextensíveis.
(c) Determinar as trações e em função de , e .
(d) Determinar as acelerações e .
Ver solução completaQuestão 3
Considere o sistema com plano inclinado envolvendo polias esquematizado na figura abaixo. Não considere atrito. Assuma também que a massa das polias e dos fios são desprezíveis em comparação às massas e dos blocos e , respectivamente. Além disso, os fios não se esticam ou se deformam em geral. Note que a polia que sustenta o bloco está conectada ao fio ligado ao bloco e, assim, essa polia não está fixa.
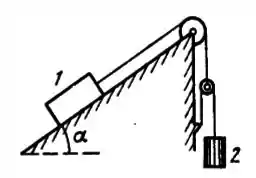
Esboce o diagrama das forças envolvidas, escreva a relação entre as diferentes tensões nos fios, e expresse a Segunda Lei de Newton para cada caso.
Demonstre a relação entre a aceleração do bloco e a aceleração do bloco .
Encontre o valor do ângulo no qual muda de sinal.
Obtenha a expressão geral para
Calcule o valor nos limites: e .
Ver solução completaQuestão 4
Considere o mecanismo apresentado na figura, onde o bloco 1 está apoiado em uma superfície sem atrito e o bloco 2 está sustentado por uma polia móvel sem massa (corpo 3 na figura). A polia fixa é ideal. O fio (ideal) conecta o bloco 1 à polia móvel e está fixo ao teto. O fio (ideal) sustenta o bloco 2 à polia 3.
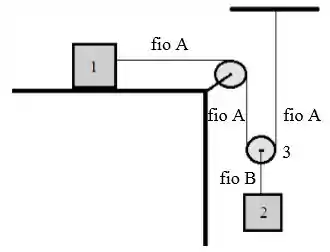
Neste mecanismo, devido ao vínculo existente entre o fio e a polia móvel, o módulo da aceleração do bloco 1, é o dobro do módulo da aceleração do bloco 2, .
As massas dos blocos são e . A massa da polia móvel . Use .
a) Represente os diagramas de corpo livre para os blocos 1 e 2 e para a polia móvel 3, explicitando todas as forças que atuam neles.
b) Escolha sistemas de coordenadas adequados para cada corpo (explicite-os!) e escreva as equações literais (não substitua ainda os valores das massas ou !) resultantes das leis de Newton para os três corpos.
c) A partir das equações do item obtenha literalmente e então substitua os valores fornecidos para encontrar o valor numérico do módulo de .
d) Obtenha o módulo da tração exercida pelo fio sobre o bloco 2.
Ver solução completaQuestão 5
Considere as polias e as cordas ideais para o dispositivo da figura abaixo. Despreze suas massas e o atrito das cordas com as polias. Como a polia que sustenta o bloco 2 é móvel, o módulo da aceleração do bloco 1 equivale ao dobro do módulo da aceleração do bloco 2. Adote os valores para as massas dos blocos e . A inclinação do plano é . Não há atrito entre o bloco 1 e o seu plano de apoio. Utilize .
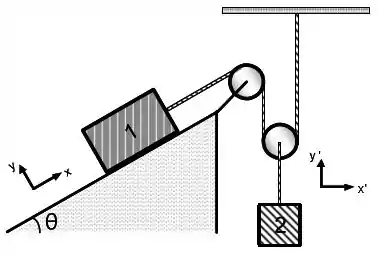
a) Represente o diagrama do corpo livre e escreva as equações de movimento em termos de suas componentes para os dois blocos e a polia móvel presa ao bloco 2. Utilize os sistemas de coordenadas fornecidos para cada componente do sistema.
b) Calcule o vetor aceleração de cada um dos blocos, usando como referência o sistema de coordenadas convencional apresentado para o bloco 2.
Ver solução completaQuestão 6
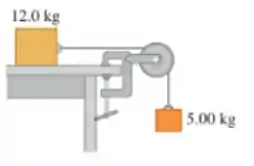
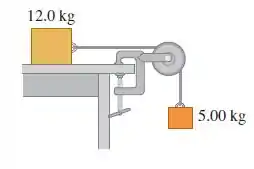
Uma caixa de em repouso sobre uma superfície horizontal e livre de atrito está atada a um peso de por um cabo delgado e leve que passa sobre uma polia com atrito desprezível (Figura abaixo). A polia possui a forma de um disco maciço e uniforme com massa de e diâmetro de . Após o sistema ser libertado, ache
c) os componentes horizontal e vertical da força que o eixo exerce sobre a polia.
Questão 7
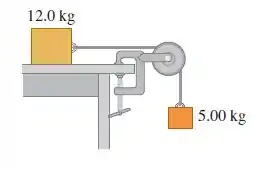
Uma caixa de em repouso sobre uma superfície horizontal e livre de atrito está atada a um peso de por um cabo delgado e leve que passa sobre uma polia com atrito desprezível (Figura abaixo). A polia possui a forma de um disco maciço e uniforme com massa de e diâmtro de . Após o sistema ser libertado, ache
a tensão no cabo sobre ambos os lados da polia
Questão 8
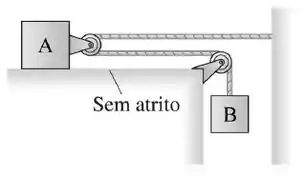
Um bloco de madeira A de massa escorrega sem atrito sobre a superfície da mesa quando puxada por uma corda sem massa onde há um corpo B pendurado de massa , como mostrado na figura. Qual é a aceleração do bloco A que desliza sobre a mesa?
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 9
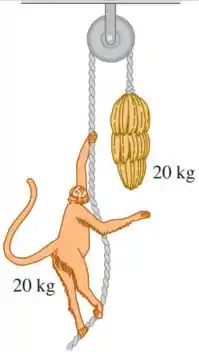
Um macaco de está segurando firmemente uma corda leve que passa sobre uma polia sem atrito e que está presa a um cacho de bananas de (Figura abaixo). O macaco olha pra cima, vê as bananas, e começa a subir a corda para ir até elas. (a) Enquanto o macaco sobe, as bananas sobem, descem ou ficam paradas? (b) Enquanto o macaco sobe, a distância entre ele e as bananas diminui, aumenta ou permanece constante? (c) O macaco solta a corda, o que acontece com a distância entre o macaco e as bananas enquanto ele cai? (d) Antes de chegar no chão, o macaco segura a corda para parar de cair. O que acontece com as bananas?
Questão 10
Três blocos estão conectados entre si por roldanas e fios ideais, como mostrado no esquema da figura . Não há atrito entre as massas e as mesas e a aceleração da gravidade é .
(c) A aceleração de cada bloco e a tensão na corda se e .
Ver solução completaQuestão 11
Três blocos estão conectados entre si por roldanas e fios ideais, como mostrado no esquema da figura . Não há atrito entre as massas e as mesas e a aceleração da gravidade é .
(a) Considere , ou seja, que as massas e são iguais. Determine:
i) A razão entre as acelerações das massas e ;
ii) A aceleração de ;
iii) A tensão no fio.
Ver solução completaQuestão 12
Uma caixa de em repouso sobre uma superfície horizontal e livre de atrito está atada a um peso de por um cabo delgado e leve que passa sobre uma polia com atrito desprezível (Figura abaixo). A polia possui a forma de um disco maciço e uniforme com massa de e diâmtro de . Após o sistema ser libertado, ache
a aceleração da caixa
Questão 13
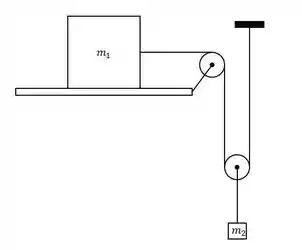
Se a superfície da figura abaixo é lisa, a aceleração do bloco será:
A.
B.
C.
D.
E.
Ver solução completaQuestão 14
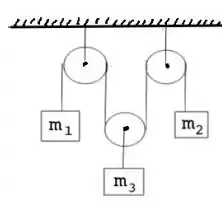
No sistema da figura , e e as massas das polias e das cordas são desprezíveis. Calcule as acelerações e das massas e e a tensão na corda.
Questão 15
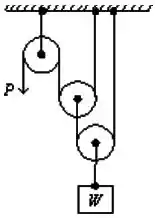
A vantagem mecânica ideal (isto é, a razão entre o peso W e a tração P necessária para o equilíbrio) da combinação de polias mostrada é:
a) 4;
b) 3;
c) 2;
d) 1;
e) 5;
Ver solução completaQuestão 16
Três blocos estão conectados entre si por roldanas e fios ideais, como mostrado no esquema na figura . Não há atrito entre as massas e as mesas e a aceleração da gravidade é .
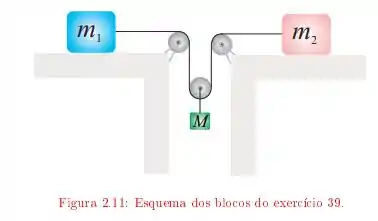
Suponha agora que as massas sejam todas diferentes. Determine
A relação entre as acelerações das massas , e ;
A aceleração de ;
A tensão no fio.
Ver solução completa