Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 13.Exercício - Ex. 46
46. Uma pequena esfera de massa está presa em uma barra de comprimento com um pivô em sua extremidade superior, formando um pêndulo simples. O pêndulo é puxado lateralmente até um ângulo com a vertical e a seguir é libertado a parti do repouso. Desenhe um diagrama mostrando o pêndulo logo após o instante em que ele é libertado. No diagrama, desenhe vetores representando as forças que atuam sobre a esfera e a aceleração da esfera. A precisão é importante! Nesse ponto qual é a aceleração linear da esfera? Repita a parte para o instante que o pêndulo forma um ângulo com a vertical Repita a parte para o instante em que o pêndulo está na direção vertical. Nesse ponto, qual é a velocidade linear da esfera?
Passo 1
Para saber a aceleração linear, temos que lembrar que a única aceleração presente em um pêndulo é a gravidade, assim a componente linear da aceleração é:
A outra coisa que temos que fazer é desenhar os diagramas do pêndulo.
Para achar a velocidade linear pedida em , vamos usar a conservação de energia mecânica, da seguinte maneira:
Onde a energia inicial é a energia do pêndulo antes de ser largado onde só temos energia potencial, a energia final é quando o pêndulo está na posição referida no item , onde só temos energia cinética, então ficamos com:
Assim basta isolar a velocidade na expressão.
Passo 2
Vamos logo isolar a velocidade na última equação do passo , assim:
Passo 3
Agora vamos desenhar os diagramas, primeiro o caso do item , assim:
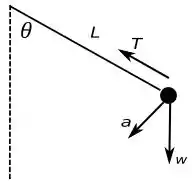
Passo 4
Agora vamos desenhar o diagrama do item , assim:
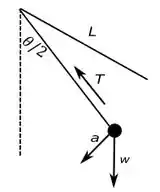
Passo 5
Agora vamos desenhar o diagrama do item , assim:
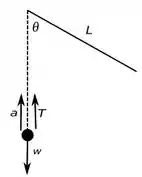
Resposta
Ei, a resposta está no passo a passo :)