Exercícios de Pêndulos Simples - Lista de Exercícios Resolvida
Questão 1
A Figura mostra um pêndulo de comprimento com uma bolinha de massa . A bolinha é presa a uma mola de constante de força , como mostrado. Quando a bolinha está diretamente abaixo do suporte do pêndulo, a mola está frouxa.
Seja o ângulo entre a haste a vertical. Para muito pequeno:
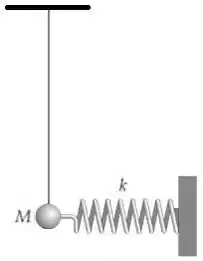
Calcule o período do pendulo.
Ver solução completaQuestão 2
Marque a alternativa ERRADA a respeito do comportamento de um pêndulo simples, na aproximação de pequenos ângulos.
- Se dobrarmos o comprimento da corda do pêndulo, o seu período também vai dobrar.
- O período não depende das condições iniciais.
- A velocidade máxima de oscilação não depende do valor da massa do pêndulo.
- Um mesmo pêndulo na lua oscila com menor frequência do que na terra sob as mesmas condições iniciais.
Questão 3
Qual a frequência de um pêndulo simples de de comprimento:
- Em uma sala.
- Em um elevador acelerando pra cima a
- Em queda livre.
Questão 4
Em que ponto do movimento de um pêndulo simples a tração no fio atinge o valor máximo? E o valor mínimo?
Ver solução completaQuestão 5
Dois pêndulos de comprimentos e oscilam de tal modo que os dois pesos em suas extremidades aproximam-se, sem se tocar, sempre que decorrem seis períodos do pendulo menor e quatro períodos do pendulo maior. Qual relação ?
Questão 6
Um pêndulo simples de comprimento L e massa M oscila com período T. Qual será o novo período se dobrarmos o comprimento L e a massa M?
a) 4T
b) 2T
c) T
d) T
e) T/4
Ver solução completaQuestão 7
Dois pêndulos de comprimentos e oscilam de tal modo que os dois pesos em suas extremidades aproximam-se, sem se tocar, sempre que decorrem seis períodos do pendulo menor e quatro períodos do pendulo maior. Qual relação ?
Questão 8
Marque a alternativa ERRADA a respeito do comportamento de um pêndulo simples, na aproximação de pequenos ângulos.
- Se dobrarmos o comprimento da corda do pêndulo, o seu período também vai dobrar.
- O período não depende das condições iniciais.
- A velocidade máxima de oscilação não depende do valor da massa do pêndulo.
- Um mesmo pêndulo na lua oscila com menor frequência do que na terra sob as mesmas condições iniciais.
Questão 9
Considere dois pêndulos simples, de mesmo comprimento presos a um mesmo ponto como mostra a figura. A partícula de massa é solta do repouso a uma altura em relação a posição de equilíbrio e atinge a partícula de massa em Anteriormente, a partícula de massa estava em repouso, na posição de equilíbrio. Após a colisão as duas partículas permanecem juntas. Considere a aceleração da gravidade conhecida e que, tanto antes quanto depois da colisão, vale a aproximação de pequenos ângulos para ambos os pêndulos.
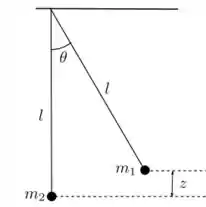
- Calcule a frequência angular do sistema após a colisão.
- Obtenha as condições inicias do sistema em
- Calcule a amplitude do sistema após a colisão.
Questão 11
Um certo pêndulo simples possui na Terra um período igual a 1,60 s. Qual é o período na superfície de Marte?
Ver solução completaQuestão 12
II – A figura abaixo mostra que, se pendurarmos um bloco na extremidade de uma mola de constante elástica k, a mola sofrerá um alongamento h = 4 cm. Se puxarmos o bloco ligeiramente para baixo a partir da posição de equilíbrio e depois liberarmos, ele oscilará com certa frequência. Qual deve ser o comprimento de um pêndulo simples para que oscile com a mesma frequência?
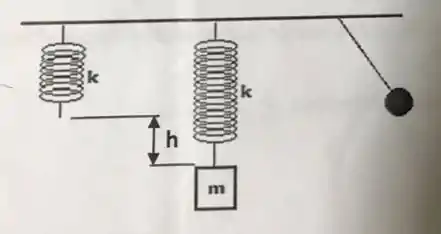
Questão 13
Dois pêndulos simples, e , possuem comprimentos e e massas e , respectivamente. Ambos executam um movimento harmônico simples. Se o período do pêndulo é o dobro do período do pêndulo , podemos afirmar que
(A) e
(B) e
(C) para qualquer que seja a razão
(D) para qualquer que seja a razão
(E) para qualquer que seja a razão
Ver solução completaQuestão 14
Um astronauta na superfície da Lua foi capaz de medir o raio da Lua (denominado por ) e agora deseja realizar um experimento para medir a sua massa. Para isso, o astronauta em questão prende uma massa em um fio de comprimento e mede o seu período de oscilação (garantindo que o ângulo de oscilação é sempre pequeno). A expressão que relaciona a massa da Lua, , e o período de oscilação do pêndulo, , é dada por
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 15
O pêndulo da figura abaixo é formado por uma haste rígida de massa desprezível, com uma bola de massa em sua extremidade. A bola na extremidade do pêndulo descreve um arco de círculo de raio que atinge a sua altura máxima no ponto B.
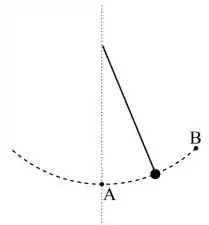
Sobre o movimento do pêndulo, escolha a alternativa correta:
(A) A velocidade da bola é nula no ponto A.
(B) A aceleração da bola é nula no ponto B.
(C) A velocidade da bola é nula no ponto B.
(D) Em toda a trajetória, a aceleração da bola aponta para o centro do círculo.
(E) Em toda a trajetória, a aceleração da bola aponta verticalmente para baixo.
Ver solução completaQuestão 16
Seja um pêndulo simples de massa , e comprimento de fio inextensível (desprezível) igual a . O mesmo é posto a oscilar em pequeno ângulo, a frequência dessa oscilação em Hz é aproximadamente de:
- 0,45
- 0,27
- 0,53
- 0,72
- 0,29
Questão 17
Uma massa suspensa por um fio está em repouso na posição de equilíbrio quando em recebe um impulso que faz com que se mova no sentido anti-horário (positivo), atingindo um ângulo máximo de . Suas oscilações subsequentes levam dois segundos para completar cada ciclo. A função que descreve corretamente seu movimento é:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 18
Um pêndulo simples formado por uma esfera de massa suspensa por um fio vertical encontra-se em repouso. Uma bala de espingarda de chumbinho, de massa , atinge a esfera horizontalmente e fica alojada nela.
O gráfico abaixo representa a posição angular do conjunto pêndulo-bala em função do tempo.
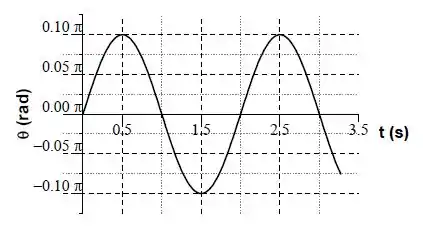
- Encontre o ângulo máximo () e a frequência angular () desse movimento.
- Escreva uma expressão literal para a função . Encontre a constante de fase e escreva os valores numéricos de todos os parâmetros dessa expressão (com unidades).
- Determine o comprimento do pêndulo e a velocidade máxima que ele atinge.
- Calcule a velocidade da bala imediatamente antes de atingir o pêndulo.
Questão 19
O pêndulo A mostrado na figura consiste em uma esfera muito pequena de massa sustentado por uma corda de massa desprezível e comprimento . O pêndulo B consiste em uma esfera muito pequena de massa e uma barra delgada de massa e comprimento L. Sejam e os tempos que cada pêndulo demora em completar uma oscilação. Para deslocamentos pequenos em relação à posição de equilíbrio, pode-se dizer que:
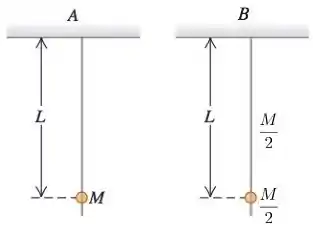
(a) Os dois pêndulos levam o mesmo tempo para completar uma oscilação, com .
(b) O pêndulo B demora menos tempo que o pêndulo A em completar uma oscilação, com .
(c) O pêndulo B demora menos tempo que o pêndulo A em completar uma oscilação, com
(d) O pêndulo B demora mais tempo que o pêndulo A em completar uma oscilação, com .
(e) O pêndulo B demora mais tempo que o pêndulo A em completar uma oscilação, com .
Formulário:
- Momentos de inércia de uma barra delgada de massa M e comprimento L em relação a um eixo que passa perpendicularmente:
- Teorema dos eixos paralelos: .
– Pelo centro de massas da barra: .
– Por uma das extremidades da barra: .
Questão 20
Um pêndulo de de comprimento é deslocado lateralmente até um ângulo de e então é liberado.
Quanto tempo leva o peso do pêndulo para atingir a velocidade mais elevada?
Ver solução completaQuestão 21
Um pêndulo de de comprimento é deslocado lateralmente até um ângulo de e então é liberado.
Quanto tempo levaria se o pêndulo fosse liberado em um ângulo de ?
Ver solução completaQuestão 22
O comprimento de um fio de pêndulo simples aumenta ligeiramente quando há um aumento na temperatura. Os ponteiros de um relógio de parede avançam devido ao movimento oscilatório do pêndulo. Supondo que os ponteiros executam um movimento harmônico simples, podemos então dizer que em dias mais quentes,
(A) o relógio marcará a hora corretamente pois a massa não muda.
(B) o relógio irá adiantar.
(C) o relógio irá atrasar.
(D) temos que saber a massa do pêndulo para poder responder.
(E) o relógio marcará a hora corretamente pois a amplitude da oscilação não muda.
Ver solução completaQuestão 23
Considere dois pêndulos simples, de mesmo comprimento presos a um mesmo ponto como mostra a figura. A partícula de massa é solta do repouso a uma altura em relação a posição de equilíbrio e atinge a partícula de massa em Anteriormente, a partícula de massa estava em repouso, na posição de equilíbrio. Após a colisão as duas partículas permanecem juntas. Considere a aceleração da gravidade conhecida e que, tanto antes quanto depois da colisão, vale a aproximação de pequenos ângulos para ambos os pêndulos.
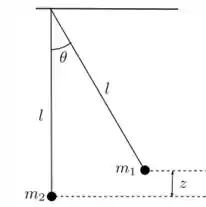
- Calcule a frequência angular do sistema após a colisão.
- Obtenha as condições inicias do sistema em
- Calcule a amplitude do sistema após a colisão.
Questão 24
(Cap 13 - Ex 45) Uma maçã pesa . Quando você a suspende na extremidade de uma mola longa de massa desprezível e constante igual a , ela oscila para cima e para baixo com um . Quando você interrompe a oscilação e deixa a maçã oscilar lateralmente em um ângulo pequeno, a frequência do pêndulo simples é igual à metade da frequência da oscilação vertical. (Como o ângulo é pequeno, a oscilação lateral não produz variação no tamanho da mola.) Determine o comprimento da mola quando ela não está esticada (sem a maçã).
Ver solução completaQuestão 25
Em que ponto do movimento de um pêndulo simples a tração no fio atinge o valor máximo? E o valor mínimo?
Ver solução completaQuestão 26
Um pêndulo simples tem comprimento L e período natural de pequenas oscilações T. Quando ele passa por sua posição de equilíbrio, a corda é repentinamente presa no seu ponto médio. O período então torna-se:
- Nenhuma das alternativas
- T/2
- 2T
- T/4
- T
Questão 27
Um peso desconhecido é preso a uma das extremidades de uma mola e prova uma elongação da mola de uma distância , na posição de equilíbrio. Mostre que, nestas condições, se o peso for colocado para oscilar em MHS, o período é o mesmo de um pêndulo simples de comprimento .
(Obs: considere a mola de massa desprezível).
Ver solução completaQuestão 28
Um pêndulo é formado por um fio ideal de comprimento e uma partícula de massa . Ele é afastado de um ângulo no sentido positivo da posição de equilíbrio e abandonado a partir do repouso, realizando pequenas oscilações que podem ser tratadas como harmônicas simples. Sua energia cinética como função do tempo é dada pela função:
a)
b)
c)
d)
Ver solução completaQuestão 29
Considere 3 pêndulos de torção, de massa m. O primeiro é formado por disco suspenso pelo centro, o segundo por uma esfera oca e o terceiro por uma barra, suspensa pelo centro. O diâmetro e o disco da esfera é igual comprimento da barra. Os três fios são iguais. Qual(is) o pêndulo que oscila mais depressa?
- o que contém o disco.
- Todos oscilam com mesma frequência
- Os pêndulos que contêm o disco e a barra, que oscilam com mesma frequência.
- o que contém a esfera.
- o que contém a barra.
Questão 30
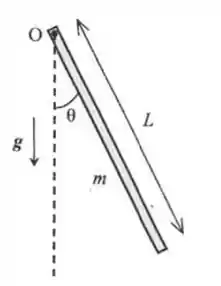
O pêndulo físico ilustrado na figura ao lado é composto por uma barra retilínea e homogênea, de comprimento e massa . Tal pêndulo oscila sob ação da gravidade em torno da sua posição de equilíbrio (linha tracejada vertical), tendo como ponto de suspensão o ponto , localizado no extremo superior da barra. Considere que a aceleração da gravidade no local é constante e representada por , como ilustrada na figura. Despreze quaisquer efeitos de atrito e resistência do ar. Nestas circunstâncias:
(a) Calcule o momento de inércia I deste pêndulo físico com relação ao ponto de suspensão . Dado: o momento de inércia da barra com relação a um eixo perpendicular à barra (ou seja, ao plano da página) e passando pelo seu centro de massa é
(b) Calcule o torque da força peso em relação ao ponto de suspensăo para o caso em que a barra faz um ângulo com a vertical. Expresse seu resultado para em termos de , e.
(c) Considere a aproximação de pequenas oscilações (onde ) e use a segunda lei de Newton para rotações para mostrar que o ângulo satisfaz uma equação do tipo oscilador harmônico. Em seguida, use tal equação para calcular o período das pequenas oscilações deste pêndulo fisico. Expresse seu resultado para em termos de e .
Questão 31
Você recebeu a missão de usar um pêndulo simples para medir o valor local de g, a aceleração da gravidade. Considere os seguintes parâmetros:
(1) comprimento do pêndulo;
(2) massa do objeto pendurado na ponta do pêndulo;
(3) período do pêndulo;
(4) amplitude da oscilação do pêndulo.
Quais desses parâmetros você teria que conhecer para calcular o valor de g?
- (1), (2) e (4).
- Apenas (2).
- (1) e (3).
- Apenas (1).
- (3) e (4).
Questão 32
Para que o período de um pêndulo simples, de comprimento L, seja dobrado devemos aumentar o comprimento do pêndulo de:
- 2L
- 4L
- 6L
- 5L
- 3L
Questão 33
A massa do peso de um pêndulo é m, e a massa de um bloco pendurado em uma mola também é m. A constante elástica da mola é escolhida para que o pêndulo e o bloco oscilem coma mesma frequência. O que acontece com os dois sistemas se as duas massas forem aumentadas para 2m?
- A frequência dos dois sistemas diminui.
- A frequência dos dois sistemas aumenta.
- A frequência do pêndulo diminui e a frequência do bloco permanece a mesma.
- A frequência do bloco aumenta e a frequência do pêndulo permanece a mesma.
- A frequência do bloco diminui e a frequência do pêndulo permanece a mesma.
Questão 34
Diante de cada afirmação, responda ou corrija aquelas que estiverem errados e justifique com suas palavras o seu raciocínio.
Considere um pêndulo de uma massa que oscila, pendurada por um fio sem massa e de comprimento constante. A velocidade da massa é nula nas extremidades do arco (pontos A e B), mas a aceleração se anula no ponto onde a velocidade, é máxima (C)
Ver solução completaQuestão 35
A Figura mostra um pêndulo de comprimento com uma bolinha de massa . A bolinha é presa a uma mola de constante de força , como mostrado. Quando a bolinha está diretamente abaixo do suporte do pêndulo, a mola está frouxa.
a)Seja o ângulo entre a haste a vertical. Para pequeno temos que onde .Calcule o período do pendulo em função de .
b)O diagrama de forças é apresentado na figura ao lado. Calcule em função . Assuma que
c)A partir do resultado anterior obtenha o período do pendulo se .
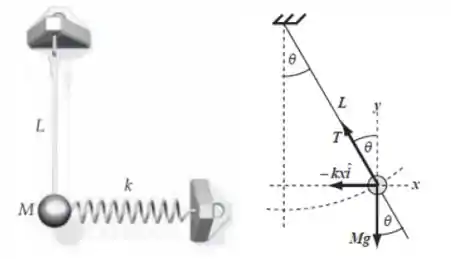
Dados: Para muito pequeno:
Ver solução completaQuestão 36
Na superfície de outro planeta foi feito um experimento para determinar a aceleração da
gravidade. Utilizando um pêndulo simples foi medido o período de oscilações para vários comprimentos como mostra o gráfico. Chamado essa gravidade em outro planeta, escreva uma expressão para descobrir esse valor através de e e use os dados do gráfico para encontrar o valor da gravidade.
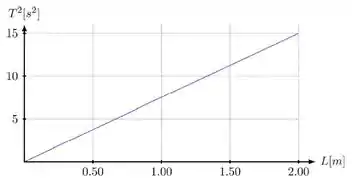
Questão 37
Um pêndulo simples, como mostrado na figura, é lançado de uma posição , com uma velocidade .
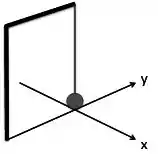
Qual é a trajetória do pêndulo, vista de cima, dados e positivos?
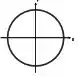 sentido anti-horário
sentido anti-horário
 sentido horário
sentido horário
 sentido horário
sentido horário
 sentido anti-horário
sentido anti-horário
Questão 38
Um pêndulo simples é formado por um fio ideal de comprimento , ligado a uma massa em uma extremidade e na outra presa a um pino na parede, de modo que ele pode girar livremente, como mostra a figura. Considere conhecida a aceleração da gravidade.
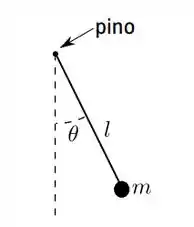
- Mostre que a energia mecânica (energia cinética + potencial) E deste sistema pode ser escrita como:
- Determine o valor da energia mecânica tal que para o movimento é ilimitado (isto é, o pêndulo pode completar uma volta completa).
- Aplicando princípios de conservação da energia, obtenha a equação de movimento para as oscilações do pêndulo.
- Obtenha o período do pêndulo na aproximação de ângulos pequenos (quando, ).
- Encontre a solução para a equação de movimento deste pêndulo om a aproximação de ângulos pequenos para encontrar o ângulo θ como função do tempo . Considere que, no instante inicial , o pêndulo se encontra na posição de equilíbrio , mas recebe um impulso de modo que a sua velocidade angular inicial é , onde é um parâmetro adimensional conhecido.
Dica: Considere a energia potencial mínima igual a zero no ponto mais baixo da tra jetória do pêndulo.