Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 10.Exercícios e Problemas - Ex. 49
49. É um belo dia com neve nova e muito lisa. Julie inicia no topo da rampa com de inclinação mostrada na FIGURA P10.49. Na base da mesma, um arco circular a conduz para cima, descrevendo , e então ela é lançada da rampa a de altura. A que distância
horizontal da extremidade da rampa ela aterrissará na neve?
Passo 1
Então galera tomando os eixos coordenados da forma tradicional, temos que para achar essa distância que o enunciado quer vamos usar a seguinte equação da cinemática:
Onde é a distância do momento que a Julie sai da rampa até ela encostar no chão.
Mas para usarmos essa equação temos que saber a velocidade dela na direção com que ela sai da rampa e tempos que saber o intervalo de tempo que levou para isso ocorrer.
Podemos encontrar a velocidade que ela sai da rampa na mesma direção diagonal que a rampa através da conservação de energia mecânica, dada por:
Onde a parte inicial é quando ela está no topo da rampa e a parte final é quando ela sai da rampa.
Lembrando que nessa situação a energia potencial é gravitacional.
Tendo a velocidade com que ela sai da rampa na diagonal é só decompor ela na direção , mas para isso precisamos saber o angula que a parte menor da rampa faz com a horizontal, isso vamos discutir mais para frente.
Agora a outra coisa que falta é o intervalo , para achar esse intervalo vamos usar a mesma equação que vamos usar para só que agora para , assim:
Onde vamos achar (velocidade com que ela sai da rampa na direção ) da mesma forma que só precisamos do ângulo o valor de é igual a , é a posição de Julie quando ela toca o chão e é a posição quando ela sai da rampa.
Passo 2
Vamos então encontrar primeiro a velocidade com que a Julie deixa a rampa, temos o seguinte:
No momento inicial ela está em repouso logo , então temos que:
Dividindo os dois lados por , temos:
Substituindo os valores que conhecemos, temos:
Então temos que:
Passo 3
Agora antes de continuar com o desenvolvimento da questão vamos encontrar aquele ângulo que comentei lá em cima com você.
Se você reparar no desenho do enunciado podemos meio que fechar um quadrado, certo?
Onde um dos lados faz um ângulo de com a horizontal e o outro é o outro é o que queremos saber.
Quando temos uma linha horizontal passando por um quadro bem alinhado da maneira como mostra a figura abaixo temos um ângulo de de cada lado somando .
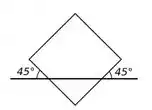
Então se o quadro estiver um pouco torto como o do caso enunciado, temos que o ângulo que queremos saber vai ser o seguinte:
Agora que temos esse ângulo, vamos continuar o nosso problema.
Passo 4
Vamos agora encontrar o intervalo de tempo que comnetei no passo , para a gente achar esse valor vamos usar a seguinte equação:
Onde teremos que e (pois aponta para baixo no sentido negativo de ), substituindo os valores que conhecemos, temos:
O que temos aqui é uma equação do segundo grau e já estamos cansados de resolver equações desse tipo, então temos o seguinte:
Então temos que:
Ou
Mas como estamos tratando de intervalo de tempo não tem como termos resultado negativo, logo
Passo 5
Agora só nos resta encontrar a distância que Julie percorreu na direção até tocar o chão. Temos a seguinte equação:
Um detalhe a ser mencionado é que em um movimento em duas direções caso não tenha nada impulsionando o objeto na direção não teremos aceleração nessa direção.
E lembrando também que , temos o seguinte:
Agora substituindo os valores que temos, ficamos com: