Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 10.Exercícios e Problemas - Ex. 62
62. Prótons e nêutrons (conjuntamente chamados de núcleons) são mantidos juntos dentro do núcleo de um átomo por uma força chamada de interação forte. Para separações muito pequenas, a interação forte entre dois núcleons é mais intensa do que a força elétrica repulsiva entre dois prótons - daí seu nome. Mas a interação forte enfraquece rapidamente com o aumento da distância entre os prótons. Um modelo bem-estabelecido para a energia
potencial de dois núcleons que interagem via interação forte é dado por
onde é a distância entre os centros dos dois núcleons, é uma constante de valor e .
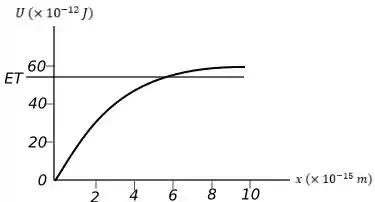
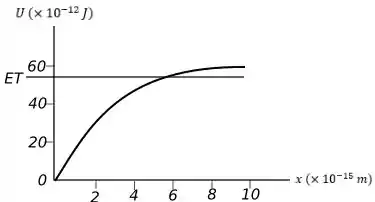
Calcule e desenhe uma curva de energia potencial acurada desde até . Calcule manualmente seu valor em pontos ou use um software de computador para tal.
Efeitos quânticos são essenciais para uma compreensão adequada do comportamento dos núcleons. Apesar disso, vamos inocentemente considerar dois nêutrons como se eles fossem pequenas esferas eletricamente neutras e duras, com massa de e diâmetro de . (Consideraremos nêutrons em vez de prótons a fim de evitar complicações advindas das forças elétricas entre os prótons.) Você segura dois nêutrons separados por uma distância de , medida entre seus centros, e depois os solta. Desenhe a linha da energia total para esta situação em seu diagrama do item .
Qual é a rapidez de cada nêutron ao colidir um com o outro? Tenha em mente que os dois nêutrons estão em movimento.
Passo 1
Então galera todo o nosso problema gira em torno da expressão de energia potencial fornecida pelo enunciado.
No item temos que desenhar um gráfico para essa energia potencial que é bem dizer um gráfico de exponencial. O s pontos que o item pede não tem necessidade de calcular já que ele diz que podemos usar software.
A situação do item inicialmente só temos a energia potencial agindo, assim basta calcular a energia potencial para essa situação e desenhar a linha que corresponde a energia que encontramos no gráfico.
Como vocês podem ver vamos primeiro vamos calcular a energia da situação do item e depois vamos desenhar o gráfico pedido em junto com a linha que o item pede
Para o item vamos usar a conservação de energia mecânica onde inicialmente só temo a energia potencial por conta da separação entre as esferas e no final temos a energia cinética da velocidade das esferas e a energia potencial referente a separa de um diâmetro das esferas já que elas estão coladas no final.
Passo 2
Primeiro vamos encontrar a energia total da situação do item , que acaba correspondendo a energia potencial da separação entre as esferas. Temos:
Substituindo com os valores que temos, assim:
Então temos que:
Passo 3
Agora podemos desenhar o gráfico pedido em , junto com a linha pedida em , assim temos:
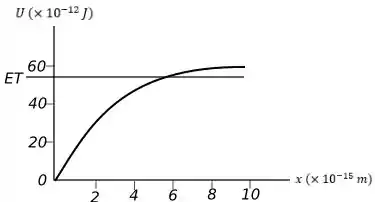
Esse é o nosso gráfico e você pode ver a linha da energia total pedida em .
Passo 4
Agora vamos para o item , onde vamos usar a conservação de energia para encontrar a velocidade das esferas, temos:
Inicialmente só temos energia potencial, então:
Temos que inicialmente temos e no final temos .
Essa energia inicial já calculamos no passo . Vamos calcular a energia potencial final agora, temos:
Então temos que:
Agora temos o seguinte então:
Lembrando que a massa das esferas vale , assim:
Então temos que:
Resposta
