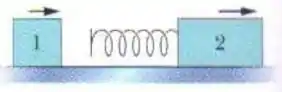
Na figura o bloco 1 (com uma massa de 6,00k g ) está se movendo para a direita a 8,0m / s e o bloco 2 (com uma massa de 4,0k g ) está se movendo para a direita a 2,0m / s . A superfície não tem atrito e uma mola com uma constante elástica de 8000N / m está presa ao bloco 2 . Em um certo instante o bloco 1 alcança o bloco 2 e começa a comprimir a mola. No momento em que o bloco 1 está se movendo para a direita a 6,4m / s , quais são (a) a velocidade do bloco 2 e (b) a energia potencial elástica da mola?

(a) A velocidade do bloco 2 é de 4,4m / s .(b) A energia potencial elástica da mola é 38J .

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.Problemas Adicionais - Ex. 126

Na figura o bloco (com uma massa de ) está se movendo para a direita a e o bloco (com uma massa de ) está se movendo para a direita a . A superfície não tem atrito e uma mola com uma constante elástica de está presa ao bloco . Em um certo instante o bloco alcança o bloco e começa a comprimir a mola. No momento em que o bloco está se movendo para a direita a , quais são (a) a velocidade do bloco e (b) a energia potencial elástica da mola?

Passo 1

(a) Qual era o momento linear inicial do sistema inteiro?

Se mais tarde o bloco estará se movendo a para a direita, essa relação tem que continuar valendo, então:

Passo 2

(b) Vamos calcular a variação de energia cinética no sistema. Comparando os dois instantes que foram mencionados no enunciado:

E mais tarde a energia cinética é:

Passo 3

Já que não temos nenhum atrito na superfície, e os blocos estão se movendo apenas na horizontal, o que podemos dizer que aconteceu com a energia cinética que sumiu do sistema?

Foi armazenada na mola, na forma de energia potencial elástica. Então, no momento mencionado no enunciado, a energia potencial elástica da mola é:

Resposta

(a) A velocidade do bloco é de .

(b) A energia potencial elástica da mola é .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um queijo de 1,20 kg é colocado sobre uma mola de massa desprezível e constante k = 1800 N/m que está comprimida 15,0 cm. Até que altura acima da posição inicial o queijo se eleva quando a mola é libe

Considere o cavaleiro do Exemplo 7.8 (seção 7.3) e a Figura 7.12. Como no exemplo, o cavaleiro é libertado a partir do repouso quando a mola está esticada em 0,100 m. Agora, porém, o ar não circula ma

Você foi solicitado para projetar uma mola que deve fornecer a um satélite de 1160 kg uma velocidade de 2,50 m/s em relação a uma estação espacial em órbita. Sua mola deve fornecer ao satélite uma ace

Considere o cavaleiro do Exemplo 7.8(Seção 7.3) e a Figura 7.12. a) Como no exemplo, o cavaleiro é libertado a partir do repouso quando a mola está esticada 0,100 m. Qual é a velocidade do cavaleiro q

Para o elevador do Exemplo 7.11 ( Seção 7.3 ) . qual é aenergia potencial armazenada na mola quando o elevador está noponto 2 indicado na Figura 7.13? b ) Ache a altura máxima que o elevador sobe a pa