Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 25.Exercício - Ex. 50
50- No circuito analisado no Exemplo ( Seção ), o resistor de é substituído por um resistor de , como no Exemplo .
Calcule a taxa de conversão da energia elétrica em energia química na bateria. Como você compara sua resposta ao resultado obtido no Exemplo
Calcule a taxa de dissipação da energia elétrica na resistência interna da bateria. Como você compara sua resposta ao resultado obtido no Exemplo
Use os resultados dos itens e para calcular a potência líquida fornecida pela bateria. Como você compara sua resposta com a energia elétrica dissipada na resistência de obtida no Exemplo
Passo 1
Aí tu vai no exemplo e ele diz para ver o exemplo e e para olhar a figura , tá quase um ARG (alternative reality game) isso aquihahaha mas o circuito é esse aqui:
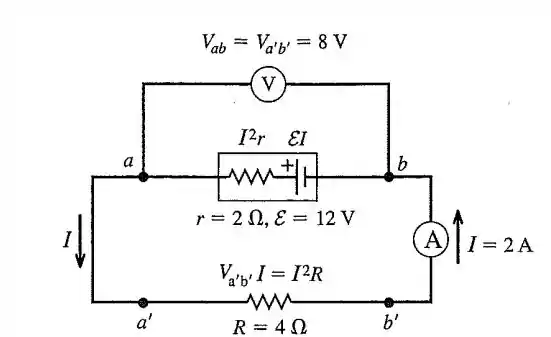
Onde agora
Como o voltímetro é ideal (nenhuma corrente passa por ele) então a corrente que passa pelo resistor será de:
Fazendo com que a potência da fonte de tensão da bateria seja de: ( sempre que você ler ‘’taxa de conversão da energia elétrica em energia química’’ entenda como potência que sai da fonte de tensão) .
E esse valor é menor que o de encontrado no exemplo . Até por conta da corrente menor.
Passo 2
A potência na resistência interna será de:
E esse valor é menor que a de encontra no exemplo .
Passo 3
Pelas duas potências que encontramos temos que a potência na carga de será:
E que faz sentido pois: