Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 54
54. Quais são as coordenadas x e y do centro de massa da chapa homogênea de aço mostrada na FIGURA P12.54?
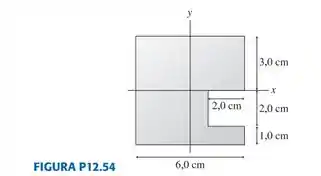
Passo 1
Para esse problema, você tem que ter em mente que o centro de massa de uma superfície homogênea, é o mesmo que o centro geométrico da figura!
ALÉM DISSO, a figura não parece ser a subtração de um retângulo por outro menor? Veja:
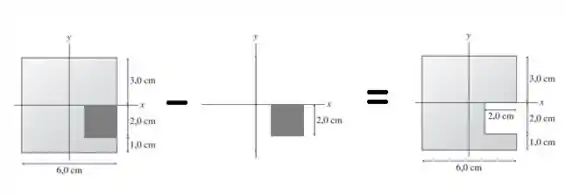
Então o centro de massa também pode ser obtido subtraindo o dentro de massa de um pelo centro de massa do outro (o quadrado menor).
Passo 2
Agora que vem o mais legal desse problema! Não precisa fazer nenhuma integral, afinal, sabemos que o centro geométrico do quadrado está no meio dela!
CENTRO DE MASSA DO QUADRADO GRANDE:
O quadrado grandão está posicionado com o meio bem na origem, logo o seu centro de massa será:
CENTRO DE MASSA DO QUADRADO PEQUENO:
Perceba que ele de e termina em , já que ele tem de lado. O que significa que o meio dele acontece em .
Já para a coordenada , como ele está posicionado logo abaixo do eixo (), a coordenada do centro dele será negativa, como é um quadrado de lado , o centro estará a , saca?
Passo 3
Com os dois centros encontrados, podemos concluir sobre o centro de massa da chapa que será:
Resposta
Centro de Massa: