Exercícios de Cálculo do Momento de Inércia de Partículas - Lista de Exercícios Resolvida
Questão 1
Considere um corpo rígido constituído por: hastes finas, rígidas, de massa desprezível e de comprimento e um conjunto de nove massas iguais a (que podem ser consideradas puntiformes) conforme a figura abaixo. O momento de inércia desse conjunto em torno do eixo é dado por:
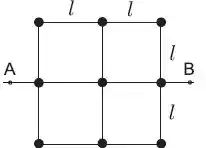
Questão 2
As massas e coordenadas de quatro partículas são as seguintes:
Quais são os momentos de inércia desse conjunto em relação ao eixos (a) , (b) e (c) ? (d) Suponha que as respostas de (a) e (b) sejam e , respectivamente. Nesse caso, qual é a resposta de (c) em termos de e ?
Ver solução completaQuestão 3
Considere um sistema de cinco objetos puntiformes dispostos em um plano de acordo com a figura a seguir. Cada um dos quatro objetos periféricos possui massa igual a , enquanto que o quinto, localizado na origem do sistema de coordenadas indicado na figura, tem massa . Eles são unidos por hastes rígidas e de massas desprezíveis.
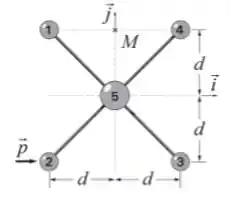
Calcule o momento de inércia do sistema em relação ao eixo passando pelos objetos e .
Calcule o momento de inércia do sistema em relação ao eixo perpendicular ao plano da figura e passando pela origem.
Calcule o momento de inércia do sistema em relação ao eixo perpendicular ao plano da figura e passando pelo ponto indicado na figura.
Ver solução completaQuestão 4
Considere um corpo rígido constituído por: hastes finas, rígidas, de massa desprezível e de comprimento e um conjunto de nove massas iguais a (que podem ser consideradas puntiformes) conforme a figura abaixo. O momento de inércia desse conjunto em torno do eixo é dado por:
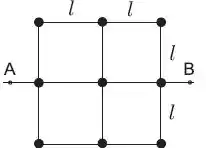
Questão 5
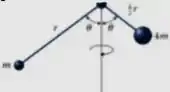
Um sistema é composto por esferas de massas: , e , conforme a Figura. O sistema gira em torno do eixo com velocidade angular , no sentido Horário pra quem vê o sistema de cima. No que segue desconsidere a Massa das hastes e considere as esferas como partículas pontuais.
- Determinar a inércia rotacional do sistema em torno do eixo
- Calcule o momento angular (módulo, direção e sentido) do sistema.
Questão 7
Um corpo rígido gira em torno de um eixo fixo com energia cinética de rotação constante. Qual das afirmações não é verdadeira?
A) Em qualquer ponto do corpo, a aceleração angular é nula.
B) Um ponto qualquer do corpo, menos no eixo fixo, possui aceleração radial.
C) Se o corpo parar de girar, seu momento de inércia se torna nulo.
D) Todos os pontos do corpo têm a mesma velocidade angular.
E) O momento de inércia é de menor valor se o corpo gira em torno de um eixo que passa pelo seu centro de massa.
Ver solução completaQuestão 8
A figura abaixo mostra um sistema de quatro partículas unidas por barras de massa desprezível rígidas. Suponha que e seja maior do que . Considere momentos de inércia em relação aos eixos cartesianos indicados na figura , como se comparam os momentos de inércia?
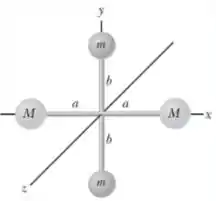
Escolha uma:
Questão 9
Qual das seguintes afirmativas concernente ao momento de inércia I é falsa ?
(A) I pode ser expresso em unidades .
(B) I depende da distribuição de massa do corpo em relação ao eixo fixo escolhido.
(C) I depende da localização do eixo fixo escolhido.
(D) I depende da orientação do eixo fixo escolhido.
(E) I é nulo em relação a um eixo fixo se o corpo não estiver em rotação.
Ver solução completaQuestão 10
Considere um corpo rígido constituído por 9 pequenas esferas de massa (que podem ser consideradas como partículas) ligadas por hastes de comprimento e massa desprezível conforme a figura.
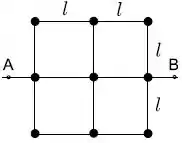
O momento de inércia desse corpo rígido em relação ao eixo é:
(a)
(b)
(c)
(d)
(e)
(f)
Ver solução completaQuestão 11
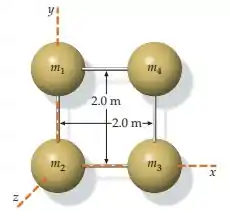
(Capítulo 9.1 – Exercício 41) Quatro partículas, uma em cada um dos cantos de um quadrado de de lado, estão ligadas por barras sem massa (figura 9-45). As massas das partículas são e . Determine o momento de inércia do sistema em relação ao eixo .
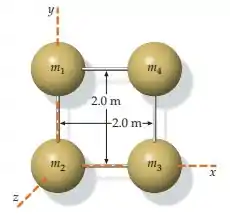
Questão 12
(Capítulo 9.1 – Exercício 41) Quatro partículas, uma em cada um dos cantos de um quadrado de de lado, estão ligadas por barras sem massa (figura 9-45). As massas das partículas são e . Determine o momento de inércia do sistema em relação ao eixo .
Questão 13
Um sistema é constituído de quatro massas iguais ligadas por arames rígidos de massas desprezíveis formando um quadrado plano de lado a, no qual as massas estão localizadas nos vértices.
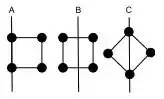
São calculados os momentos de inércia , e relativos aos respectivos eixos A, B e C, mostrados na figura. O eixo A passa lateralmente pelas duas massas, o eixo B pelo centro do quadrado a de dois lados e o eixo C na diagonal. Podemos afirmar, para os momentos de inércia , e, que
Questão 14
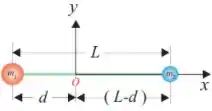
Q - Duas partículas pontuais de massas e estão conectadas por uma haste rígida (de massa desprezível) e comprimento podendo se movimentar no plano . O momento de inércia do sistema, em , em relação a um eixo perpendicular ao plano e que passa pelo centro de massa do sistema é:
Questão 15
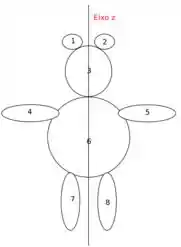
2. O momento de inércia, possui propriedades similares às do centro de massa, pois ambos são dados na forma de uma integral. Sendo assim, no cálculo do momento de inércia é possível dividir o domínio de integração em subdomínios, e posteriormente somar o resultado. Por exemplo, para a figura ao lado (um urso!), basta calcular o momento de inércia de cada uma das sub-regiões numeradas de 1 a 8 em relação ao eixo , e depois somar o resultado:
Sabendo disto, calcule o momento de inércia da figura abaixo em relação aos eixos e , supondo que as barras delgadas possuem massa desprezível, e que as barras grossas possuem massa , são homogênas e possuem secção reta circular de raio . Dados: momento de inércia de um cilindro homogêneo de massa em relação ao eixo que passa pelo centro de sua secção reta de raio e pelo seu centro de massa: ; momento de inércia de uma barra homogênea de massa e comprimento em relação ao eixo que é perpendicular à extensão da barra e passa pelo seu centro de massa: .
Questão 16
Um quadrado de massa e de lados de comprimento , tem um momento de inércia , quando rodado em torno de um eixo perpendicular à sua superfície, e que passa através do seu centro, como mostrado na figura. Agora, uma partícula, também de massa está ligada a um canto do quadrado, como mostrado. Qual é o novo momento de inércia do sistema sobre o mesmo eixo de rotação?

Questão 17
A figura mostra dois sistemas A e B que diferem apenas na distância entre as pequenas esferas colocadas na haste fixa na polia. Os dois sistemas são abandonados a partir do repouso da mesma altura em relação ao solo. Os tempos para o bloco dos sistemas A e B chegar ao solo são respectivamente tA e tB. Qual é a afirmativa correta para a relação entre estes tempos?
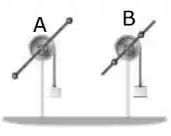
a) , porque a aceleração angular do sistema A é maior que do sistema B.
b) , porque a aceleração angular do sistema A é maior que do sistema B.
c) , porque os dois sistemas têm massas iguais.
d) , porque o torque da força peso do bloco pendurado é igual nos dois
sistemas.
e) , porque o momento de inércia do sistema A é maior que do sistema B.
Ver solução completaQuestão 18
Um fio ideal está enrolado em torno da periferia de uma polia de 0,020 m de raio. A polia está inicialmente em repouso e pode girar sem atrito em torno de seu eixo. È aplicada uma força constante de 50 N na extremidade livre do fio. Sabendo-se que o fio não desliza na polia que são desenrolados 1,2 m de fio em 4,9 s, a partir do repouso, qual é o momento de inércia da polia?
a) 0,20
b) 17
c) 14
d) 0,17
e) 0,017
Ver solução completaQuestão 19
Um arame quadrado de lado , fino, rígido e de massa desprezível, tem nos seus vértices quatro massas iguais a m. Os momentos de inércia , relativos aos respectivos eixos A, B e C mostrados na figura relacionam-se como:
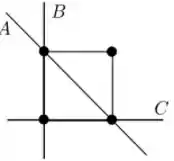
a)
b)
c)
d)
e)
f)
Ver solução completaQuestão 20
Quatro partículas de massas iguais a 1,0 kg estão ligadas por hastes rígidas e de massas desprezíveis formando um quadrado de lado 2,0m sobre um plano horizontal e sem atrito, conforme a figura. Qual é o momento de inércia do sistema em relação a um eixo perpendicular ao plano no qual se encontra o sistema e que passa pelo ponto O marcado na figura ?
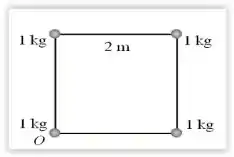
(A) 4,0 kg
(B) 8,0 kg
(C) 10 kg.
(D) 16 kg
(E) 12 kg
Ver solução completaQuestão 21
Uma barra uniforme possui duas pequenas bolas coladas às suas extremidades (Figura 1). A barra possui de comprimento e a massa de , enquanto as bolas possuem cada uma e podem ser tratadas como partículas pontuais. Ache o momento de inércia desse sistema em relação a cada um dos seguintes eixos:
b) um eixo perpendicular à barra e que passa por uma das bolas

Questão 23
Uma barra uniforme possui duas pequenas bolas coladas às suas extremidades (Figura 1). A barra possui de comprimento e a massa de , enquanto as bolas possuem cada uma e podem ser tratadas como partículas pontuais. Ache o momento de inércia desse sistema em relação a cada um dos seguintes eixos:
c) um eixo paralelo à barra e que passa por ambas as bolas

Questão 24
Qual das seguintes afirmações sobre momento de inércia de um objeto é falsa?
(A) pode ser expresso em unidades de se não usarmos o SI.
(B) depende da aceleração angular do objeto enquanto este gira em torno de um eixo fixo.
(C) depende da localização do eixo de rotação em relação às partículas constituintes do objeto.
(D) depende da orientação do eixo de rotação em relação às partículas constituintes do objeto.
(E) Das partículas constituintes do objeto, a de menor massa pode dar a maior contribuição para .
Ver solução completaQuestão 25
Uma prancha uniforme tem 6,0 m de comprimento e pesa 80 N. Ela está equilibrada na posição horizontal apoiada sobre um cavalete no seu ponto médio. Um peso de 160 N é posto na extremidade esquerda da prancha. Para manter a prancha equilibrada, de que distância o cavalete precisa ser deslocado para a esquerda?
(A) 6,0 m (B) 2,0 m (C) 1,5 m (D) 1,2 m (E) 0,50 m
Ver solução completaQuestão 26
12) Uma barra delgada e uniforme de massa e comprimento tem presa em uma de suas extremidades uma partícula de massa , como mostra a figura. Ao calcularmos o momento de inércia do sistema barra partícula em relação a um eixo passando pelo centro de massa do sistema e perpendicular à barra, encontramos
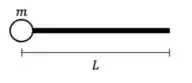
(a)
(b) (c)
(d) .
(e)
Ver solução completaQuestão 27
Os corpos estão ligados por barras muito leves cujos momentos de inércia podem ser desprezados. O sistema gira em torno do eixo y com velocidade angular.
a. Considere que no instante t = 0 s, os corpos estejam nas posições indicadas na figura. Determine o vetor velocidade de cada partícula usando o produto vetorial ⃗v = ⃗ω × ⃗r.

Questão 28
Os corpos estão ligados por barras muito leves cujos momentos de inércia podem ser desprezados. O sistema gira em torno do eixo y com velocidade angular.
b. Use a velocidade escalar de cada corpo para calcular a energia cinética do sistema.

Questão 29
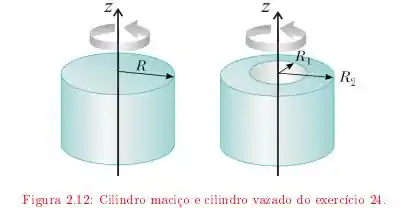
Um cilindro maciço de raio e massa tem . Utilizando este resultado, calcule o momento de inércia de um cilindro uniforme vazado de massa , de raio interno e externo , em relação ao eixo [veja a figura ].
Questão 30
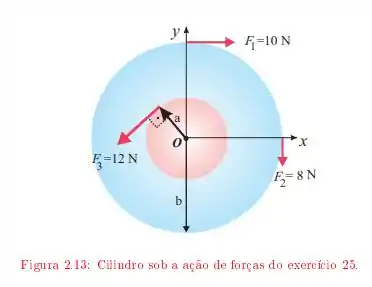
Um cilindro de massa gira em torno de um eixo que passa pelo centro. Sobre ele são aplicadas as forças indicadas na Figura onde e .
Sabendo que a velocidade angular inicial do cilindro era , determine .
Questão 31
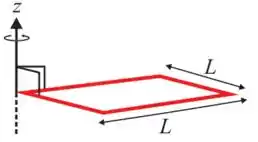
45. Um objeto quadrado de massa é formado por quatro varetas finas idênticas, todas de comprimento e massa , amarradas juntas. O objeto é fixado a uma barra, podendo girar em torno dela com velocidade angular , como mostrado na figura. O momento de inércia do objeto, em relação ao eixo de rotação (eixo z) na figura é:
(a) .
(b) .
(c) .
(d) .
(e) .
Ver solução completaQuestão 32
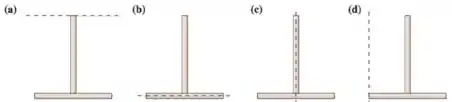
46. Duas barras idênticas, de mesma massa e comprimento, são usadas para desenhar um objeto com a forma da letra . Cada objeto pode girar em torno do eixo indicado pela linha tracejada na figura. Para os momentos de inércia a , relacionados com a rotação em torno ao eixo indicado, pode-se afirmar que:
(a) .
(b) .
(c) .
(d) .
(e) .
Ver solução completaQuestão 33
Uma barra uniforme possui duas pequenas bolas coladas às suas extremidades (Figura 1). A barra possui de comprimento e a massa de , enquanto as bolas possuem cada uma e podem ser tratadas como partículas pontuais. Ache o momento de inércia desse sistema em relação a cada um dos seguintes eixos:
a) um eixo perpendicular à barra e que passa pelo seu centro

Questão 34
Uma partícula de massa descreve uma trajetória na forma de uma circunferência de raio . Sua posição angular (em rad.) e dada pela expressão:
Com o tempo em segundos.
A energia cinética de rotação da partícula (em joules) no instante vale:
Questão 35
Uma barra uniforme possui duas pequenas bolas coladas às suas extremidades (Figura 1). A barra possui de comprimento e a massa de , enquanto as bolas possuem cada uma e podem ser tratadas como partículas pontuais. Ache o momento de inércia desse sistema em relação a cada um dos seguintes eixos:
d) um eixo paralelo à barra e a uma distância de dela.

Questão 36
Três massas, , e estão afixadas em uma barra de massa desprezível que gira em torno do eixo com velocidade angular , conforme a figura.
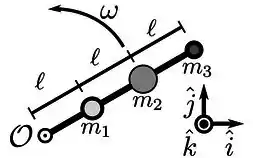
Qual o momento de inércia do conjunto de massas na figura em relação ao eixo?
Questão 37
Uma esfera e um cilindro de massas e raios iguais são soltos simultaneamente, sem velocidade inicial, em um mesmo plano inclinado e rolam para baixo. Então:
A. O cilindro alcança a base do plano primeiro porque ele adquire maior energia rotacional;
B. A esfera alcança a base do plano primeiro porque ela tem maior inércia;
C. A esfera o cilindro chegam juntos à base do plano;
D. A esfera alcança a base do plano primeiro porque ela adquire maior energia rotacional;
E. Nenhuma alternativa é correta;
Ver solução completaQuestão 38
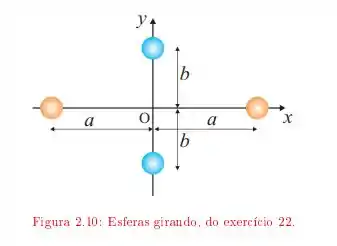
Quatro esferas pequenas de massa m estão presas às extremidades de uma estrutura de massa desprezível no plano xy.
b. Supondo que o sistema gire no plano xy ao redor de um eixo passando por O (eixo z), calcule o momento de inércia ao redor do eixo z e a energia rotacional ao redor desse eixo.
Questão 39
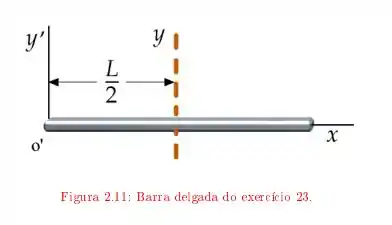
Uma barra na, com uma distribuição de massa uniforme, tem massa M e comprimento L. Calcule o seu momento de inércia em relação a um eixo (y) que passa pelo centro da barra e é perpendicular ao plano xz . Usando o teorema dos eixos paralelos, determine o momento de inércia em relação ao eixo y ′ , que passa por O′ e é paralelo ao eixo y.