Enunciado
Química - Young and Freedman - Vol 4- Ed: 12º - Capítulo 43.Problemas - Ex. 62
62. As medidas de atividade de uma amostra radioativa são indicadas na tabela abaixo. Calcule a meia-vida. Quantos núcleos radioativos estavam presentes na amostra no instante Quantos estavam presentes depois de ?
Passo 1
Então galera, vamos lá!
O tempo de meia vida pedido em pode ser encontrado de forma tranquila usando a seguinte equação:
O problema é achar esse (constante de decaimento), ele pode ser encontrado ajustando a curva dos dados fornecidos pela tabela, colocando esses dados em gráfico temos o seguinte:
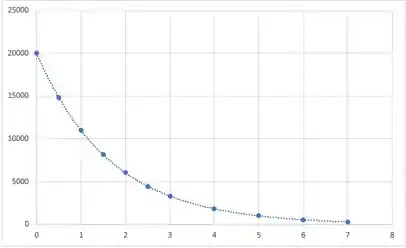
Plotando esses dados e ajustando a linha de tendência encontramos a seguinte função para esse gráfico:
Onde teremos que que é o parâmetro que determina a inclinação da curva.
Sabendo disso nossas contas ficam tranquilas.
Agora para achar quantos núcleos nós tínhamos no instante inicial, basta usarmos a equação dada por:
Não iremos usar o sinal de negativo que tem na equação pois ele será irrelevante nesse caso.
Onde vamos fazer , o parâmetro são os valores da coluna direita da nossa tabela (decaimentos por segundo), mas nesse caso iremos querer o decaimento por hora já que foi determinado em relação au tempo em horas.
E para vai ser o número de núcleos que estamos procurando.
Para achar quantos núcleos estavam presentes depois de , basta usar a equação , que ela nos fornece o número de núcleos restantes, ela é da seguinte forma:
Passo 2
Vamos as contas então, vamos achar o tempo de meia vida, temos que:
Substituindo o valor de , temos:
Passo 3
Agora vamos calcular o número de núcleos iniciais, temos que:
Onde para segundo a tabela, temos:
Mas nos interessa o decaimento por hora, assim basta multiplicar esse valor por que é a quantidade de segundos em uma hora, assim:
Agora usando a equação inicial temos que:
Passo 4
Agora vamos encontrar o número de núcleos restantes em , temos que:
Substituindo os valores que sabemos para , temos: