Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 30.Problemas - Ex. 63
63. No circuito indicado na Figura , a chave é fechada no instante sem carga inicial no capacitor. Determina a leitura em cada amperímetro e voltímetro logo após a chave ser fechada. Determine a leitura de cada instrumento após estar fechada há muito tempo. Determine a carga máxima no capacitor. Desenha um gráfico qualitativo da leitura do voltímetro em função do tempo.
Passo 1
Nesse problema temos duas situações, a primeira é quando a chave acaba de ser fechada então podemos considerar e a situação em que a chave está fechada a muito tempo, assim temos .
No primeiro caso quando a corrente no indutor é zero e a tensão no capacitor é zero.
Assim, o indutor pode ser tratado como interrupção no circuito e o capacitor pode ser substituído por um fio.
No segundo caso quando , a tensão no indutor vai a zero e não temos corrente no capacitor. O indutor pode ser substituído por um fio e o capacitor por uma interrupção no circuito.
Para achar a carga máxima no capacitor, temos que encontrar que só vai aparecer no caso de , já que a carga pode ser encontrada através da seguinte relação:
Passo 2
Vamos começar vendo tudo relacionado a situação do item .
Primeiro como o indutor funciona como uma interrupção no circuito temos que .
Conseguimos tirar também a seguinte relação através do comportamento da tenção em um circuito, temos:
Logo:
Mas no capacitor nessa situação temos que a tensão é zero, logo , então temos que
Então, sabendo que a única maneira das expressões acima serem verdadeiras é que .
Agora como todos os outros a tensão é zero, então só pode ser igual a .
Sabendo disso podemos encontrar a corrente total que passa no circuito pela lei de Ohm, temos que:
Agora para achar os valores nos amperímetros, temos que nos ligar que:
Temos que é igual a corrente total do circuito já que ele está colocado depois de todos os elementos e temos que é iguala zero pois ele está depois do indutor.
Agora, deve ser iguala acorrente total do circuito já que o capacitor está fazendo o papel de um fio, então nossa expressão acima fica da seguinte forma:
Passo 3
Agora vamos encontrar tudo relacionado ao item primeiro vamos encontrar a corrente do circuito, para isso vamos usar a lei de Ohm para o circuito equivalente que é formado pelos resistores de , e .
Com essa situação temos que a resistência equivalente é:
Então temos que:
Agora podemos encontrar a corrente, temos:
Então temos que:
Passo 4
Agora que temos o valor da corrente vamos encontrar os valores medidos nos voltímetros através da lei de Ohm.
Primeiro , temos:
Para temos que é igual a zero já que o indutor está se comportando como um fio.
Mas e , e como fica? Então, para elementos ligados em paralelo o mesmo potencial que vai para um caminho vai para o outro, como inicialmente depois de passar por ficamos com uma voltagem de , então temos que:
Logo:
Agora podemos achar os valores medidos nos amperímetros pela lei de Ohm.
Primeiro para temos que a medida é igual a zero já que o capacitor age como uma barreira.
Para os outros três amperímetros temos a seguinte relação:
Vamos encontrar a medida de , já que:
Agora encontrando a medida de . Temos:
Então temos que:
Passo 5
Agora podemos encontrar a carga máxima no capacitor temos que e carga é dada por:
Substituindo os valores que conhecemos, temos:
Passo 6
Agora para desenhar o gráfico pedido no item , temos que observar algumas coisas. Em , temos , essa tensão ela tem um crescimento e com o passar do tempo ela cai para zero, assim:
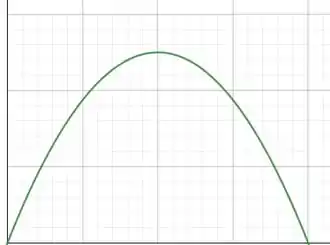
E é mais ou menos isso o que encontramos, onde a vertical se refere a voltagem e a horizontal se refere ao tempo.
Resposta
