Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.9 - Ex. 50
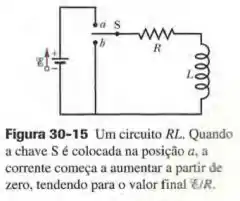
A chave da Fig. 30-15 é colocada na posição no instante . Determine a razão entre a força eletromotriz autoinduzida no indutor e a força eletromotriz da fonte (a) logo após o instante ; (b) no instante . (c) Para que múltiplo de temos ?
Passo 1
A questão fala sobre um circuito no processo de carregamento, em que a corrente está aumentando. No instante , a corrente é nula, isto é, . Assim, a tensão no resistor .
Como temos que
Segue que
Isso significa que no instante em que a chave é fechada toda a tensão do circuito está no indutor. Conforme o tempo passa e a corrente cresce, a tensão no resistor cresce e a do indutor diminui, com a soma das duas se mantendo constante!
Passo 2
No item (b), devemos calcular a tensão do indutor em . Para isso, lembre-se que a corrente é dada por
Assim,
Portanto,
Desta forma, com :
Passo 3
Por fim, no item (c) nós queremos o instante de tempo em que a razão das tensões é :
Assim, tomando o log dos dois lados
Desta forma,