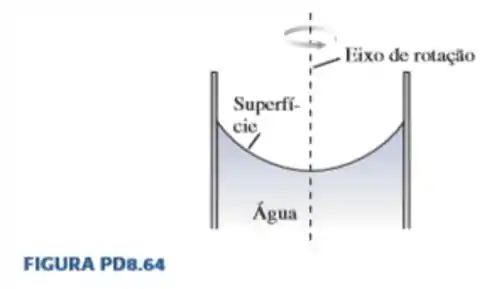
64. Se um cilindro vertical de água (ou qualquer outro líquido) gira em torno de seu eixo, como mostra a FIGURA PD8.64, a superfície forma uma curva suave. Considerando que a água gire como uma unidade (i.e., toda ela gira com a mesma velocidade angular), mostre que a forma da superfície do líquido é uma parábola descrita pela equação .
Sugestão: cada partícula de água na superfície experimenta somente duas forças: a gravidade e a força normal devido à água embaixo dela. A força normal, como sempre, é exercida perpendicularmente à superfície
Passo 1
Se liga só!
Bora dar uma ajeitadinha na nossa figura anterior... Aqui está!
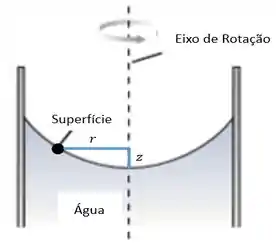
Em seguida, tomando um ponto qualquer da superfície e fazendo um diagrama de corpo livre para ele, obtemos a seguinte imagem abaixo...
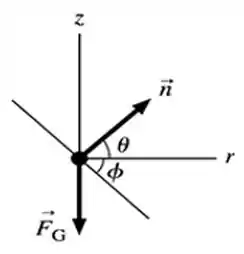
Passo 2
Em seguida, uma vez que esse ponto está em equilíbrio na direção vertical... Para o eixo , temos a seguinte equação...
Isolando :
Já para o eixo , a outra componente da normal , vai ser a responsável por puxar o ponto para o centro da trajetória em um movimento circular. Em síntese, vai ser a nossa resultante centrípeta. De modo que ficamos com...
Isolando :
Passo 3
Depois, dividindo por :
Passo 4
Agora repara só!
A curva formada pelo giro do cilindro se assemelha muito a de uma função do grau, cujo eixo de simetria passa exatamente pelo eixo .
E como essa curva tem concavidade para baixo, então nossa equação vai ser a seguinte...
Derivando em relação a ...
Essa equação descreve a localização no nosso ponto na curva!
Passo 5
E pegando o diagrama de corpo livre que fizemos, podemos ver que:
Desse modo, bora usar a aproximação abaixo para a localização do nosso ponto ...
Ficamos então, com...
E igualando essa expressão com aquela outra do , que descobrimos para ...
Isolando ...
Ficou moleza agora! Como ... Subsituindo a expressão do obtida anteriormente...
Viu só! É a mesma expressão do enunciado
Sendo assim! Missão finalizada com sucesso!