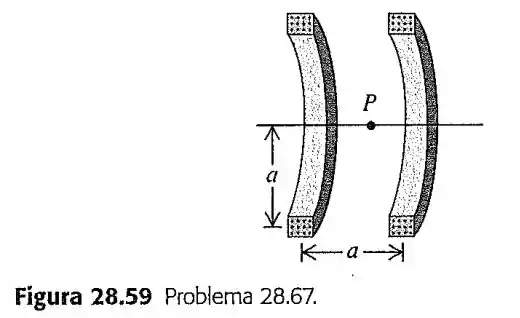
67- Bobinas de Helmhotz. A Figura mostra a seção reta de duas bobinas circulares com raio , cada uma delas com espiras que conduzem uma corrente no mesmo sentido. A distância entre as bobinas é igual ao raio das bobinas. As bobinas dessa configuração denominam-se bobinas de Helmholtz e produzem um campo magnético bastante uniforme na região entre elas.
Deduza uma expressão para o módulo do campo magnético em um ponto situado a uma distância a direita do ponto , que está no centro de simetria das bobinas.
Faça um gráfico de contra desde até . Compare o gráfico obtido com o campo magnético produzido apenas pela bobina da direita.
Usando a expressão obtida no item , obtenha o módulo do campo magnético no ponto
Calcule o valor do módulo do campo magnético no ponto , considerando
Calcule e no ponto . Discuta como seus resultados podem mostrar que o campo é bem uniforme nas vizinhanças do ponto .
Passo 1
A expressão do campo magnético produzido por uma bobina circular em um ponto fora do seu centro será:
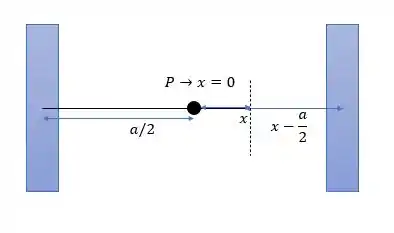
Pois cada bobina tem n espiras agora.
Portanto para a bobina a esquerda o campo magnético em um ponto será:
E para a bobina a direita há ponto :
Logo o campo magnético total em é a soma das duas (pois no centro de seu eixo as duas sempre apontarão na mesma direção). Então:
Passo 2
Considerando uma constante qualquer temos que o gráfico de seja:
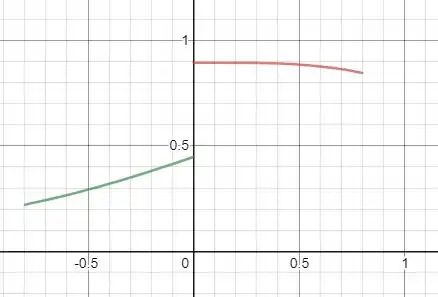
Onde o gráfico em vermelho é do campo total e o verde o da bobina a direita. O da bobina em direita nós consideramos negativo pois a distância em a direita de está a esquerda da bobina a direita.
Passo 3
Para a letra basta fazermos , pois é a origem da nossa referência.
Então:
Agora aplicando , nós teremos um módulo de campo em igual a:
Passo 4
Derivando em essa equação gigantesca:
Pela substituição e aplicando regra da cadeia. Então para nós teremos:
O que zera.
Agora para teremos:
Essa já precisa de um capricho um pouco maior para conseguir ver. Mas se aplicarmos nessa equação nós veremos que:
O que no gráfico para o total de pode ser entendido melhor como:
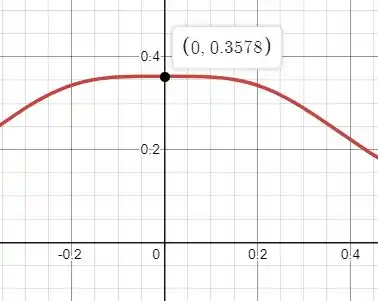
Logo as proximidades de ou no ponto o campo magnético se mantém bem uniforme, já que ele não cresce por e nem muda de concavidade, sendo parecido com uma reta constante de fato.