Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Problemas - Ex. 77
Um cilindro comprido, com seu eixo orientado ao longo do eixo , possui uma densidade de corrente . A densidade de corrente, embora seja simétrica em relação ao eixo do cilindro, não é constante e varia de acordo com a relação
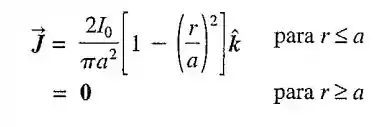
Em que é o raio do cilindro, é a distância radial entre o ponto considerado e o eixo do cilindro e é uma constante dada em ampéres.
Mostre que é a corrente total que passa através da seção reta do fio
Usando a lei de Ampére, deduza uma expressão para o módulo do campo magnético na região .
Obtenha uma expressão para a corrente contida em uma seção reta circular de raio e centralizada sobre o eixo do cilindro.
Aplicando a lei de Ampére, deduza uma expressão para o módulo do campo magnético na região . Como se comparam os resultados dos itens e para
Passo 1
Vamos dividir a seção reta do fio cilíndrico em diversas seções circulares de espessura de forma que:
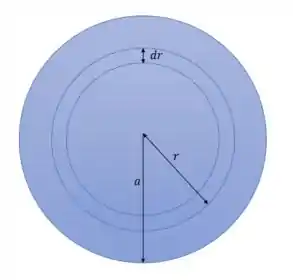
Onde se mantém de acordo com uma fórmula pré-estabelecida e é o elemento de área dessa espessura de disco e que será (imagine um retângulo de comprimento , onde os dois comprimentos dos círculos são bem parecidos, com uma altura , logo:
Onde é dada no enunciado
Então:
Integrando de 0 até a nós teremos:
Então para o raio igual a (que é o que abrange todo o círculo da seção reta do fio) nós teremos passando uma corrente .
Passo 2
Para uma região fora da seção reta do fio nós teremos:
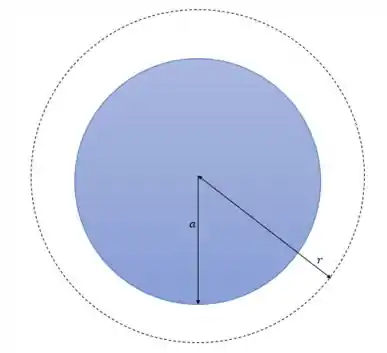
E como nessa região somente temos uma corrente então pela lei de Ampere teremos:
Passo 3
Agora para nós teremos a seguinte situação:
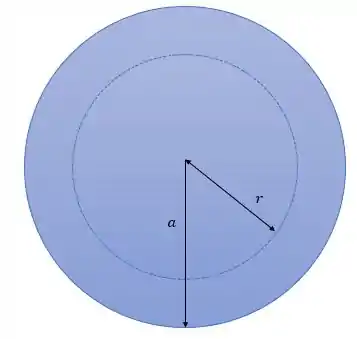
Nessa situação nós deveremos encontrar a corrente na seção de até em função de ao fazer a integral:
Só que agora de até , o que nos dará:
Passo 4
Agora a equação do campo magnético para um , sabendo que nessa região passa uma corrente igual a :
Se aplicarmos para esse campo interno nós teremos:
Agora para o campo encontrado na letra :
Nos dando dois resultados iguais, tanto para externo ao fio quanto ao interno.