Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 73
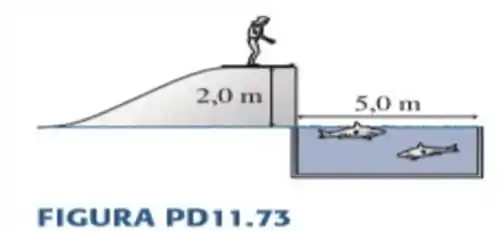
73. Você pegou um emprego de verão em um parque aquático. Em um número de acrobacia, uma esquiadora desliza até o topo da rampa livre de atrito e com de altura da FIGURA , e depois salta sobre um tanque com de largura cheio de tubarões famintos. Você irá pilotar a lancha que impulsionará a esquiadora sobre a rampa. Ela soltará as duas cordas quando estiver na base da rampa, exatamente no momento em que você faz a curva de volta. Qual é máxima velocidade que você deve ter ao chegar à rampa a fim de que a esquiadora sobreviva para o show de amanhã?
Passo 1
Opa! Aqui vamos nós de novo!
Olha só! Pra entender melhor esse problema, vamos começar fazendo um esboço mais ou menos do que tá acontecendo ou melhor do que precisa acontecer pra que nosso amigo não vire comida de tubarão.
Passo 2
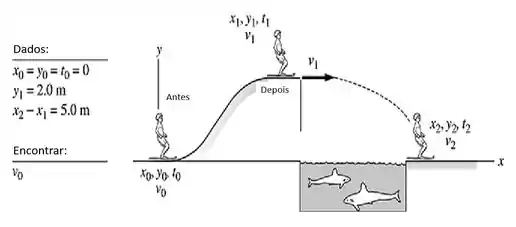
Pelo que podemos ver da figura anterior, o nosso amigo sai de e salta até cair em ... Ou seja, ele excecuta o que chamamos de movimento oblíquo, que é composto de um movimento uniforme, na direção horizontal, e de um movimento acelerado, na vertical.
No caso do moviment vertical, uma vez que ele sai de até chegar em . Vamos usar a equação abaixo, do movimento acelerado...
Onde a aceleração , é na verdade, a aceleração da gravidade, com sinal negativo porque aponta para baixo e o sentido positivo do nosso referencial é para cima.
Uma vez que a componete vertical da velocidade no instante é nula. Ficamos com...
Passo 3
Na direção horizontal, em , o nosso movimento é uniforme. Sendo assim, usemos a equação abaixo...
Bom! Como o tanque tem de largura. Logo, e precisam estar espaçados por no mínimo, . O que nos leva à:
Desse modo, sabendo o intervalo de tempo... Conseguimos que a velocidade de lançamento horizontal vai valer:
Como só existe a componente horizontal da velocidade nesse instante...
Passo 4
Finalmente, uma vez que sabemos o valor da velocidade em , para encontrar a máxima velocidade que deve-se ter ao chegar à rampa, bastar usar a conservação da energia mecânica...
Em , temos apenas a presença de energia cinética. Já em , temos tanto energia cinética como potencial presentes, uma vez que a esquiadora está com velocidade numa altura de .
Logo,
Isolando ...
E depois substituindo os valores numéricos correspondentes...
Essa deve ser a velocidade no início da rampa!
Pronto! Até que enfim alcançamos nossa resposta!