Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 7.Problemas Adicionais - Ex. 81
81- No sistema massa-mola da Fig. 7-10, a massa do bloco é 4,00 kg e a constante elástica da mola é 500 N/m. O bloco é liberado da posição . Determine (a) a velocidade do bloco no ponto x = 0, (b) o trabalho realizado pela mola quando o bloco chega ao ponto x = 0, (c) a potência instantânea desenvolvida pela mola no momento em que o bloco é liberado, (d) a potência instantânea desenvolvida pela mola quando o bloco está passando pelo ponto x = 0 e (e) a posição do bloco no instante em que a potência desenvolvida pela mola é mínima.
Passo 1
Vamos colocar aqui a figura só para sabermos do que se trata.
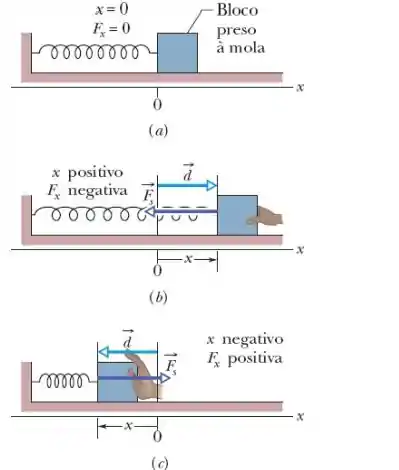
Na posição inicial a energia é puramente elástica, tendo como módulo igual a:
b) Com e temos o trabalho da mola da sua posição de origem até igual a:
No ponto de toda essa energia elástica vira energia cinética, logo:
Já que a massa é de .
Passo 2
A potência é calculada pela seguinte fórmula.
c)E no instante em que ela é solta a sua velocidade inicial é de , logo a potência nesse instante será de 0 W
d) Quando passa pela posição de a massa terá uma velocidade de só que a força atuando sobre ela é de , já que a mola não estará esticada então a potência nesse instante também será de
Passo 3
A potência de qualquer corpo pode ser calculada pela equação.
Como interessados na potencia elástica nós temos que saber que a equação da força elástica vale:
Pois a força da mola somete depende da posição final da mola em relação a posição inicial que é em .
E que a velocidade pode ser adquirida pela energia cinética
Logo:
Considerando podemos calcular a potencia instantânea que será:
Derivando em relação a essa equação (uma vez que é um valor constante) nós encontraremos:
Para encontrarmos a potência mínima precisamos igualar-la a zero, isso nos dá:
Como temos:
Assumindo não está em zero, temos:
Isso nos faz encontrar: