Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 72
Em cada um dos Problemas de 69 a 72, é fornecida uma ou mais equações para resolver um problema. Em cada um deles, você deve
a. Redigir um problema realista para o qual a(s) equação(ções) seja(m) apropriada(s).
b. Desenhar uma representação pictórica correspondente.
c. Resolver o problema proposto.
72.
Passo 1
Opa! Aqui vamos nós de novo!
a) Olha só! Pela equação do nosso problema, da pra ver que o nosso corpo está em um movimento vertical.
E dessa vez não temos nem presença de força normal nem de atrito. Pelo menos não, pelo que observamos da nossa equação.
Quanto a equação de potência, podemos ver que o na real é a potência gerada pela força , sendo que o nosso corpo se move a num determinado instante.
Pronto! Matamos o problema!
Acho que com esse três dados importantes! Dá pra ver que o problema basicamente vai ser um corpo sendo tracionado para cima.
Não esquecendo que pela equação, podemos tirar que a massa do corpo é de e pelo jeito, vai descer apenas devido ao efeito da aceleração da gravidade
Desse modo! Propomos o seguinte problema...
“Um bloco de está sendo acelerado para cima a por um cabo. Quanta energia o motor deve fornecer no instante em que a velocidade é de ? ”
b) E aqui está um esboço pra ajudar melhor na compreensão do problema...
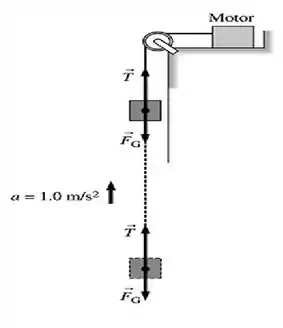
Passo 2
c) Feito o esboço, bora aproveitar a imagem anterior, onde as forças já estão indicadas para usar a segunda lei de Newton, uma vez que o nosso bloco está acelerado para cima com ...
Substituindo os valores que temos...
Obtemos a primeira equação. Resolvendo-a...
E a potência gerada por essa força de tração, é simplesmente o produto dela pela velocidade num determinado instante. No nosso caso, essa velocidade é de ...
Essa é a segunda equação... Que ao ser resolvida nos fornece que;
Resposta
a)
“Um bloco de está sendo acelerado para cima a por um cabo. Quanta energia o motor deve fornecer no instante em que a velocidade é de ? ”
b)
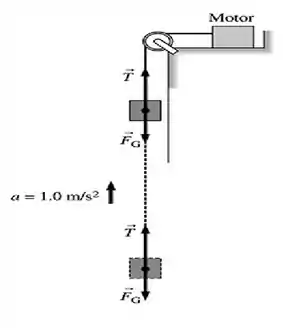
c)