Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 76
76. A equação mgy para a energia potencial gravitacional é válida somente para objetos próximos à superfície de um planeta. Considere dois objetos muito grandes, de massas e , tais como estrelas e planetas, cujos centros estão separados por uma grande distância r. Esses dois grandes objetos exercem forças gravitacionais um sobre o outro. No Capítulo 13, você aprenderá que a energia potencial gravitacional é dada por
onde é chamada de constante da gravitação universal.
a. Esboce um gráfico de versus A dificuldade matemática em não constitui um problema físico significativo porque as massas colidirão antes de seus centros se aproximarem muito.
b. Que separação foi escolhida como a situação em que a energia potencial é nula? Isso faz sentido? Explique.
c. Duas estrelas encontram-se em repouso relativo, separadas por . Isso corresponde a aproximadamente vezes o diâmetro do Sistema Solar. A primeira delas é do tamanho do Sol, com uma massa dee um raio de . A segunda estrela possui uma massa de e um raio de . Elas se atraem por forças gravitacionais. Quais serão os valores de velocidade das estrelas no momento do impacto?
Passo 1
a) Aqui vamos nós! Olha só! O que a gente tem que fazer aqui, é esboçar o gráfico de em função de , baseado na fórmula abaixo...
Pela fórmula, considerando constante, podemos ver que se aumentar, a distância irá diminuir.
Se ocorrer o contrário e diminuir, é porque irá aumentar. Logo, dá pra deduzir que o nosso gráfico é uma hipérbole, o mesmo gráfico por exemplo, para a equação abaixo...
Cuja forma já estamos cansados de saber.
Sendo assim, o nosso gráfico de versus fica do seguinte modo...
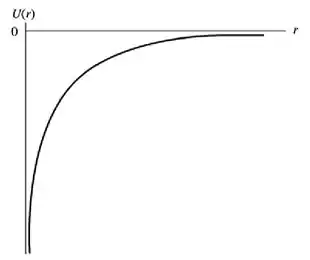
Uma vez que o sinal da nossa fórmula é negativo, todos os valores de energia potencial são negativos. Isto é claro, para .
Passo 2
b) Em seguida, vamos determinar a situação em que a energia potencial é nula.
Bem! Peguemos a fórmula abaixo.
E depois peguemos um valor de muito grande, lá na casa dos ! O que vai acontecer!?
Ora bolas! A energia potencial vai diminuir bastante! De forma que se aproxima de zero!
Sendo assim, fica moleza compreender que se tenter ao infinito , ira acontecer o seguinte...
E é nessa situação que a energia potencial será nula.
Passo 3
c) Essa letra aqui vai dar um pouquinho mais de trabalho...
Por isso, vamos fazer um desenho pra representar o que está acontecendo em nosso probleminha...
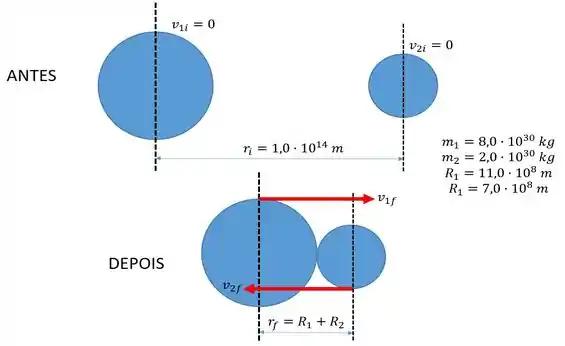
Bom! Podemos ver que pela figura temos um antes e um depois. É a situação perfeita pra aplicar a conservação de energia mecânica! Fazendo isso...
Lembrando que a nossa energia potencial aqui, é a energia potencial gravitacional. Dito isso, a nossa fórmula anterior passa a ter a seguinte cara...
Como...
Rearrajando a expressão...
Obtemos uma relaçãoazinha legal! Mas ainda não podemos obter nada, pois ainda estamos em função de duas variáveis.
Passo 4
Sendo assim, vamos aplicar a conservação do momento linear...
Como...
Então...
Substituindo em :
Isolando :
E subsituindo os valores numéricos adequados, que estão naquele belíssimo esboço que fizemos...
Obtemos o valor da velocidade da estrela de maior massa!
Em seguida, pegando a equação :
Aproveitando apenas o valor absoluto...
Conseguimos a outra velocidade para a estrela de menor massa!
E pronto! Finalizamos aqui!
Resposta
a)
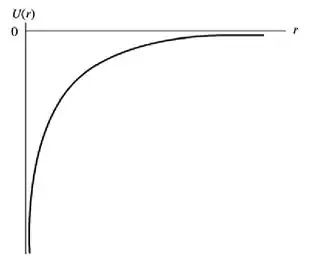
b)
c)