Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 12.Questões Conceituais - Ex. 3

3. A FIGURA Q12.3 mostra três discos em rotação, todos de mesma massa. Ordene em seqüência decrescente as energias cinéticas de rotação de K a a K c .

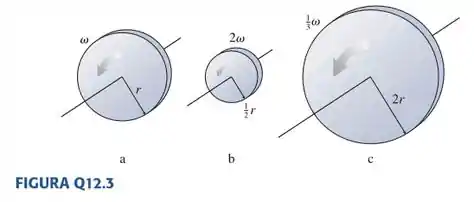
Passo 1

Bom! Nós sabemos que a energia cinética de rotação é dada por...

K r o t a ç ã o = I ω 2 2

Quanto ao momento de inércia, como todas as figuras tratam-se de discos... O momento de inércia de um disco em relação a um eixo perpendicular ao centro de massa, é dado por:

I d i s c o = 1 2 m r 2

Sendo assim, a energia cinética do disco a , de raio r girando com velocidade angular ω , vale...

K a = I a ω a 2 2

K a = m r 2 ω 2 2

Já a energia cinética do disco b , de raio r / 2 e girando com velocidade angular 2 ω , é igual a:

K b = I b ω b 2 2

K b = m ⋅ ( r / 2 ) 2 ⋅ ( 2 ω ) 2 2

K b = m r 2 ω 2 2

E por último, a energia cinética do disco c , de raio 2 r e girando com velocidade angular ω / 3 ...

K c = I c ω c 2 2

K c = m ⋅ ( 2 r ) 2 ⋅ ( ω / 3 ) 2 2

K c = 2 m r 2 ω 2 9

Sendo assim, obtemos que as energias cinéticas rotacionais dos discos a e b são iguais e também maiores que a do disco c .

K a = K b > K c

Resposta

K a = K b > K c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No sistema indicado na Figura 9.18, uma massa de 12,0 kg é libertada do repouso e cai, fazendo com que o cilindro uniforme de 10,0 kg e diâmetro de 30,0 cm gire em torno de um eixo sem atrito que pass
Um ônibus de passageiro em Zurique, na Suíça, usa sua potência motora oriunda da energia acumulada em um volante grande. Utilizando-se de energia da rede elétrica, a roda é colocadaem movimento period
Dois discos metálicos, um com raio R 1 = 2,50 c m e massa M 1 = 0,80 k g e o outro com raio R 2 = 5,0 c m e massa M 2 = 1,60 k g , são soldados juntos e montados em um eixo sem atrito passando pelo ce
No cilindro junto com a massa do Exemplo 9.9 (Seção 9.4), suponha que a massa m que cai seja feita de borracha, de modo que nenhuma energia mecânica é perdida quando a massa atinge o solo. a) Supondo
Uma barra uniforme de comprimento L repousa sobre uma superfície horizontal sem atrito. A barra possui um pivô, de modo que ela pode girar sem atrito em torno de um eixo passando por uma das suas extr