Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 20

Uma partícula que se move ao longo do eixo y tem energia potencial U = 4y³ J, onde y está em metros. a. Desenhe o gráfico da energia potencial desde y = 0 m até y = 2 m. b. Qual é o componente y da força exercida sobre a partícula em y = 0 m, 1 m e 2 m?

Passo 1

Foi dado como a energia potencial de uma partícula varia conforme ela se move no eixo y. A energia potencial está relacionada com a força que está atuando na partícula pela importante relação:

F = - d U d y

Assim, sabendo como varia a energia potencial em função da posição, saberemos a força que está atuando sobre a partícula.

Passo 2

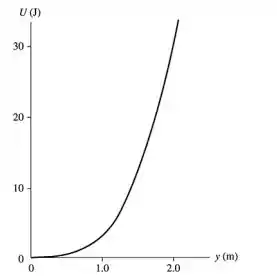
  1. Esse item pede para desenharmos o gráfico de U em função de y para y = 0 até y = 2   m . Note que U = 4 y 3 é uma função do tipo polinomial de grau 3. Seu gráfico está representado abaixo.

    2. Passo 3

  2. Vimos, no passo 1, que

F = - d U d y F = - d d y 4 y 3 F = - 4 d d y y 3 F = - 4 ⋅ 3 ⋅ y 3 - 1 F = - 12 y 2

onde nas contas acima usamos as seguintes regras de derivação:

  1. Uma constante pode “sair” da derivada;
  2. Regra do tombo: d d y y n = n y n - 1 (“tomba” o expoente e tira 1).

Portanto, já sabemos como F varia com y . Assim, podemos calcular tal força em y = 0 ,   1   e   2 m :

  • Em y = 0 , temos F = - 12 ⋅ 0 2 = 0 N.
  • Em y = 1   m , temos F = - 12 ⋅ 1 1 = - 12   N .
  • Em y = 2   m , temos F = - 12 ⋅ 2 2 = - 48   N .

Resposta

0 N, -12 N e -48 N.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma força F → = 3,00N i ^ + 7,00N j ^ + 7,00N k ^ age sobre um objeto de 2,00k g que se move de uma posição inicial d → i = 3,00m i ^ - 2,00m j ^ + 5,00m k ^ para uma posição final d → f = - 5,00m i ^
Um funny car acelera a partir do repouso, percorrendo uma certa distância no tempo T , com o motor funcionando com potência constante P . Se os mecânicos conseguem aumentar a potência do motor de um p
Um objeto de 2,0k g inicialmente em repouso acelera uniformemente na horizontal até uma velocidade de 10m / s em 3,0s . (a) Nesse intervalo de 3,0s , qual é o trabalho realizado sobre o objeto pela fo
A potência da luz solar que atinge cada metro quadrado da superfície da Terra em um dia claro nos trópicos está perto de 1000W . Em um dia de inverno em Manitoba, a concentração de potência da luz sol
A potência da luz solar que atinge cada metro quadrado da superfície da Terra em um dia claro nos trópicos está perto de 1000W . Em um dia de inverno em Manitoba, a concentração de potência da luz sol