Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 19
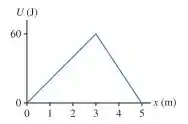
Uma partícula possui a energia potencial representada na FIGURA EX11.19. Qual é o componente x da força exercida sobre a partícula em x = 1 m e x = 4 m?
Passo 1
Foi dado o gráfico de versus a posição e nos foi pedido a força que atua sobre a partícula. Qual propriedade devemos usar para calcular tal força? Vamos usar a seguinte propriedade: a força é o negativo da derivada de em relação a . Em linguagem matemática, temos:
Porém, geometricamente, o que quer dizer uma derivada? Quando calculamos a derivada de uma curva em um ponto , estamos calculando também o coeficiente angular da reta tangente à curva nesse ponto ; porém quando a “curva” na verdade é uma reta (como no caso dessa questão), o coeficiente angular da reta tangente é na verdade o coeficiente angular da própria reta!
Assim, se calcularmos o coeficiente angular da reta, vamos conseguir obter a força.
Passo 2
Quando em , temos:
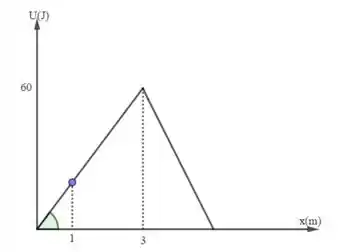
O coeficiente angular será igual a tangente do ângulo assinalado na figura. Pela trigonometria do triângulo retângulo, temos que:
Ou seja, temos que:
Passo 3
Quando em , temos
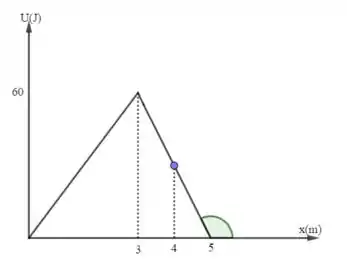
O coeficiente angular será a tangente do ângulo assinalado. Note que tal tangente é negativa, pois a reta é decrescente.
Portanto, segue que:
Resposta
-20 N e 30 N.