Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 18

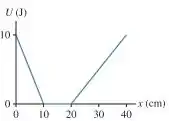
Uma partícula possui a energia potencial representada na FIGURA EX11.18. Qual é o componente x da força exercida sobre a partícula em x = 5 cm, 15 cm, 25 cm e 35 cm?

Passo 1

Vamos lembrar da relação entre energia potencial e força. A força é o negativo da derivada da energia potencial em relação à posição. Ou seja:

F = - d U d x

Graficamente o que representa uma derivada? A derivada representa o coeficiente angular da reta tangente a um determinado ponto do gráfico de U . Quando o gráfico de U for uma reta, a derivada irá representar o coeficiente angular dessa própria reta.

Passo 2

Quando x = 5   c m , estaremos localizados no ponto A :

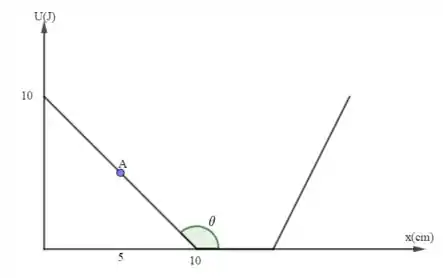
O coeficiente angular da reta (ou seja, a derivada d U / d x será igual à tangente do ângulo θ (lembremos de passar de cm para m; assim 10 cm = 0,1 m)

tan ⁡ θ = - c a t e t o   o p o s t o c a t e t o   a d j a c e n t e d u d x = - 10 0,1 = - 100

Portanto,

F = - d U d x F = 100   N

Passo 3

Quando x = 15 cm estaremos no ponto B abaixo.

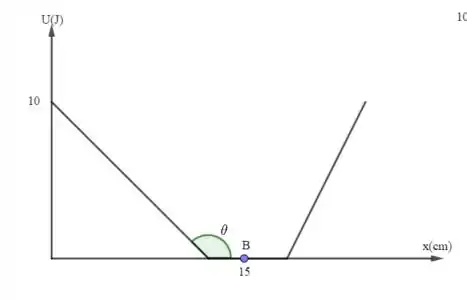
Nesse caso, o gráfico é horizontal (constante), de modo que

d U d x = 0

Logo,

F = - d U d x F = 0

Passo 4

Quando x = 25   c m e x = 35   c m estaremos sob a mesma reta; assim o coeficiente angular será o mesmo de modo que a força será a mesma em ambos casos. Agora, estaremos no ponto C :

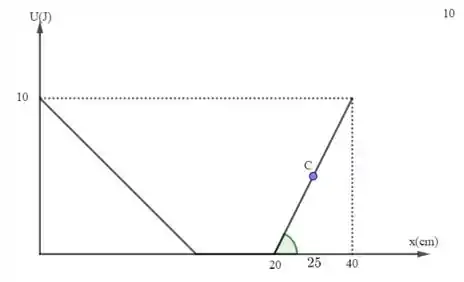
O coeficiente angular será igual à tangente do ângulo assinalado na figura acima (lembrando de passar cm para m; assim 40 cm = 0,25 m). Temos:

tan ⁡ θ = 10 0,4 - 0,2 d U d x = 50

Portanto,

F = - d U d x F = - 50   N

Resposta

-100 N; 0; -50 N e -50 N.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bandeja de 0,30k g escorrega sobre uma superfície horizontal sem atrito presa a uma das extremidades de uma mola horizontal ( k=500N / m ) cuja outra extremidade é mantida fixa. A bandeja possui u
Um elevador carregado tem uma massa de 3,0 *10 3k g e sobe210m em 23s , com velocidade constante. Qual é a taxa média com a qual a força do cabo do elevador realiza trabalho sobre o elevador?
Uma força de 5,0N age sobre um corpo de 15k g inicialmente em repouso. Calcule o trabalho realizado pela força (a) no primeiro, (b) no segundo e (c) no terceiro segundo, assim como (d) a potência inst
Um elevador de carga totalmente carregado tem uma massa total de 1200k g , que deve içar 54m em 3,0m i n , iniciando e terminando a subida em repouso. O contrapeso do elevador tem uma massa de apenas
Um esquiador é puxado por uma corda para o alto de uma encosta que faz um ângulo de 12 ° com a horizontal. A corda se move paralelamente à encosta com uma velocidade constante de 1,0m / s . A força da