A aceleração de uma paraquedista que pula de um avião é dada por , onde é uma constante positiva que depende da área da seção reta da paraquedista e da densidade da atmosfera ao seu redor. A direção é vertical para baixo.(a) Se a rapidez inicial dela é zero ao sair do helicótero, mostre que a sua rapidez como função do tempo é dada por , onde é a rapidez terminal dada por , e é um parâmetro de escala temporal. (b) Qual fração da rapidez terminal representa a rapidez em ? (c) Use um programa de planilhas para fazer o gráfico de como uma função do tempo, usando uma rapidez terminal de (use esse valor para calcular e ). A curva resultante faz sentido?
Passo 1
(a) Vamos reescrever a função usando a definição da aceleração:
E podemos resolver essa equação diferencial para encontrar :
E substituindo com a informação dada no enunciado:
Integrando dos dois lados:
E consultando essa integral em uma tabela ficamos com:
E para isolar , primeiro precisamos isolar a função trigonométrica:
Agora aplicando a função dos dois lados:
Que é exatamente a função que queríamos demonstrar.
Passo 2
(b) Quando , temos o seguinte resultado:
Portanto em , a rapidez instantânea é da rapidez terminal.
Passo 3
Agora vamos fazer um gráfico dessa função, usando :
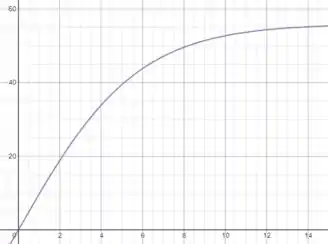
O mesmo gráfico pode ser feito em um programa de planilhas, basta aplicar a função para diversos pontos no intervalo de tempo.
Esse gráfico faz sentido, já que o gráfico se aproxima cada vez mais da rapidez terminal, sem nunca ultrapassá-la.
Resposta
(a) Demonstração.
(b) A rapidez é da rapidez terminal.
(c) Gráfico.