Exercícios de Vetor Velocidade e Aceleração Instantânea - Lista de Exercícios Resolvida

Uma partícula tem uma aceleração constante . No tempo , a velocidade é zero e o vetor posição é . Encontre os vetores velocidade e posição em função do tempo . Encontre a equação da trajetória (de em função de ) da partícula no plano e esboce a trajetória.

Sabendo-se que a posição de uma partícula, em relação à origem do plano , é determinada pelo vetor:

Com em metros () e em segundos (), determine:

O vetor velocidade instantânea e o vetor aceleração instantânea em função do tempo.

O vetor velocidade instantânea no ponto e o vetor aceleração instantânea no ponto , ambos os pontos estão indicados no gráfico abaixo. Neste gráfico, a curva contínua representa a trajetória da partícula, descrita através do vetor posição

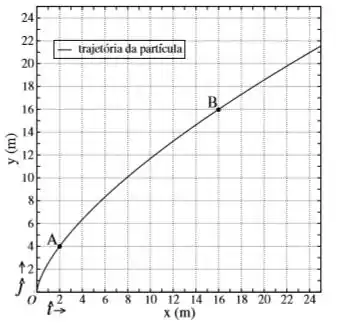
O vetor velocidade média e o vetor aceleração média , ambos entre os pontos e .

A posição de uma partícula em metros é descrita pelo vetor posição .

A velocidade e a aceleração instantânea da partícula em é

a)

b)

c)

d)

e)

f)

(g)

Uma partícula tem uma aceleração constante . No tempo , a velocidade é nula. Encontre o vetor velocidade em função do tempo .

Uma partícula movimenta-se em linha reta segundo a relação: , onde r é a distância, em metros e t é o tempo em segundos. Qual é a aceleração quando t=3?

A posição de uma partícula em metros é descrita pelo vetor posição .

Considere as afirmativas abaixo:

() A partícula passa pela origem do sistema de coordenadas.

() A tangente do ângulo entre o vetor velocidade e o eixo em é .

() O movimento da partícula não é acelerado.

Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).

(a)

(b)

(c)

(d) e

(e) e

(f) e

(g) Todas

(h) Nenhuma

O vetor posição de uma partícula é dado por , em metros, para t medido em segundos. Para o instante , os vetores velocidade e aceleração dessa partícula se escrevem:

a)

b)

c)

d)

e)

O vetor posição de uma partícula que se move no plano é dado por:

Onde é dado em metros e em segundos. Determine:

O vetor velocidade instantânea da partícula, seu módulo e direção (ângulo em relação ao eixo ) para o instante ;

O vetor aceleração instantânea da partícula, seu módulo e direção (ângulo em relação ao eixo ) para o instante ;

O vetor deslocamento da partícula no intervalo de tempo até ;

O vetor velocidade média da partícula no intervalo de tempo até .

Dado:

Um designer de páginas web criou uma animação em que um ponto na tela do computador tem posição .

(b) Encontre a magnitude e direção da velocidade instantânea em e.

O vetor posição de uma partícula que se move no plano é dado por:

Onde é dado em metros e em segundos. Determine:

(a) o vetor velocidade instantânea da partícula, seu módulo e direção (ângulo em relação ao eixo ) para o instante ;

(b) o vetor aceleração instantânea da partícula, seu módulo e direção (ângulo em relação ao eixo ) para o instante ;

(c) o vetor deslocamento da partícula no intervalo de tempo até ;

(d) o vetor velocidade média da partícula no intervalo de tempo até .

Dado:

O vetor posição de uma partícula que se move no plano é dado por:

Onde é dado em metros e em segundos. Determine:

(a) o vetor velocidade instantânea da partícula, seu módulo e direção, para o instante .

(b) o vetor aceleração instantânea da partícula para o instante .

(c) o vetor deslocamento da partícula entre os instantes de tempo e .

(d) o vetor velocidade média da partícula no intervalo de tempo e .

Se e o vetor posição de uma partícula, cujas coordenadas são dadas em metros e o tempo em segundos, determine o valor da coordenada do vetor aceleração, em , quando .

(a)

(b)

(c)

(d)

(e)

Uma partícula descreve a seguinte trajetória:

O ângulo formado entre a posição e a velocidade da partícula no instante é:

a) 45°

b)

c)

d)

e)

O vetor posição de uma partícula é dado por , para medido em segundos. Para o instante , os vetores velocidade e aceleração desta particular se escrevem:

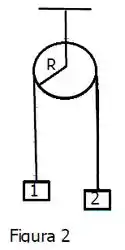
Dois blocos com massas e estão conectados um ao outro por meio de uma corda com massa desprezível que passa por uma polia de massa com formato de um disco rígido de raio (Figura 2). Encontre a aceleração dos blocos e as tensões na corda. (Assuma que não há deslizamento entre a corda e a polia.)

Uma partícula A move-se ao longo da reta , com uma velocidade constante (m/s). Uma segunda partícula, B, começa a movimentar-se, a partir da origem, com velocidade inicial nula e com aceleração constante , tal que , no mesmo instante em que a partícula A passa pelo eixo y. Qual deve ser o valor do ângulo θ, entre o vetor e o eixo y, para que, nesta situação, ocorra uma colisão entre A e B? Em que posição a colisão ocorreu?

Uma partícula percorre, com velocidade constante e no sentido anti-horário, uma circunferência de raio igual a e completa uma volta em segundos. A partícula passa pelo ponto em . Tomando a origem em , de acordo com a figura , determine:

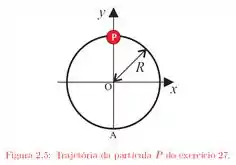
(d) A velocidade instantânea e a aceleração instantânea para e .

A posição de uma partícula que se move em um plano é dada por , com em metros e em segundos. Na notação de vetores unitários, calcule: (a) , (b) e (c) . (d) Qual é o ângulo entre o sentido positivo do eixo e uma reta tangente á trajetória da partícula em ?

As posições de um objeto em movimento bidimensional são dadas pelo vetor posição: , onde todas as quantidades estão no sistema internacional de unidades. Qual é o ângulo que o vetor velocidade faz com o eixo no instante após iniciado o movimento?

(A)

(B)

(C)

(D)

(E)

(Cap 3 – Ex 51) Uma partícula tem um vetor posição dado por onde r está em metros e t em segundos. Encontre os vetores velocidade instantânea e aceleração instantânea como funções do tempo t.

A velocidade de uma partícula que se move no plano é dada por , com em metros por segundo e ) em segundos . (a) Qual é a aceleração no instante ? (b) Em que instante (se isso é possível) a aceleração é nula? (c) Em que instante (se isso é possível) a velocidade é nula? (d) Em que instante (se isso é possível) a velocidade escalar da partícula é igual a ?

Uma partícula se move de tal forma que a posição (em metros) em função do tempo ( em segundos) é dada por Escreva expressões para (a) a velocidade e (b) a aceleração em função do tempo.

Uma partícula deixa a origem com uma velocidade inicial e uma aceleração constante . Quando a partícula atinge o máximo valor da coordenada , quais são (a) a velocidade e (b) o vetor posição?

[ENUNCIADO COMUM ÀS QUESTÕES 3 e 4]

A posição de uma partícula em metros é descrita pelo vetor posição .

[QUESTÃO 3]

Considere as afirmativas abaixo:

() A partícula passa pela origem do sistema de coordenadas.

() A tangente do ângulo entre o vetor velocidade e o eixo em é .

() O movimento da partícula não é acelerado.

Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).

(a)

(b)

(c)

(d) e

(e) e

(f) e

(g) Todas

(h) Nenhuma

[ENUNCIADO COMUM ÀS QUESTÕES 3 e 4]

A posição de uma partícula em metros é descrita pelo vetor posição .

[QUESTÃO 4]

A velocidade escalar da partícula em é

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Uma partícula executa movimento cujo vetor posição é dado por com e , sendo . Marque o vetor abaixo que é ortogonal ao vetor aceleração da partícula.

(a)

(b)

(c)

(d)

(e)

Baseado em suas experiências dirigindo automóveis, estime o módulo da aceleração média de um carro quando

acelera numa rodovia a partir do repouso até .

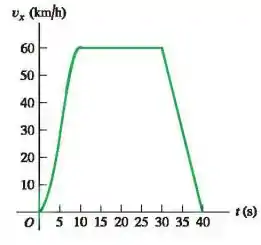
A figura abaixo mostra a velocidade de um carro movido à energia solar como uma função do tempo. O motorista acelera a partir de uma placa de pare, dirige por com velocidade constante de e começa a frear até o repouso após deixar a placa de pare.

Calcule a aceleração média durante os seguintes intervalos:

(i) ;

(ii) ;

(iii) ;

(iv) .

A aceleração de uma partícula é dada por

Encontre a velocidade inicial tal que a partícula tenha coordenada horizontal em igual a que teria em

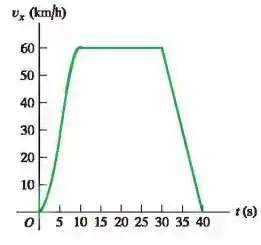
A figura abaixo mostra a velocidade de um carro movido à energia solar como uma função do tempo. O motorista acelera a partir de uma placa de pare, dirige por com velocidade constante de e começa a frear até o repouso após deixar a placa de pare.

Qual a aceleração instantânea para e para ?

Baseado em suas experiências dirigindo automóveis, estime o módulo da aceleração média de um carro quando

Explique por que a aceleração média em cada caso pode ser considerada positiva ou negativa.

A aceleração de uma partícula é dada por

Qual será a velocidade em ?

Baseado em suas experiências dirigindo automóveis, estime o módulo da aceleração média de um carro quando

freia até parar subitamente.

A posição de um elétron que se move ao longo do eixo é dada por , onde está em segundos. A que distância da origem se encontra o elétron quando para momentaneamente?

O vetor velocidade de uma partícula é (SI). Qual é o valor da aceleração no tempo ?

A.

B.

C.

D.

E.

Um próton move-se ao longo do eixo x de acordo com a equação , onde x está em

metros e t em segundos. Calcule

(a) a velocidade média do próton durante os primeiros 3 segundos de seu movimento;

(b) a velocidade instantânea do próton em t = 3 s;

(c) a aceleração instantânea do próton em t = 3 s.

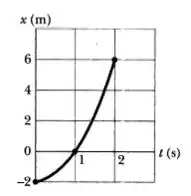
(d) Trace o gráfico x(t) e indique como a resposta do item (a) pode ser obtida

deste gráfico.

(e) Indique a resposta do item (b) gráfico.

(f) Trace gráfico v(t) e indique nele a resposta do item (c).

A Figura abaixo descreve o movimento de uma partícula movendo-se ao longo do eixo com uma aceleração constante. Quais são o

(a) módulo e

(b) o sentido da aceleração da partícula?