Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.Problemas - Ex. 94

Acelerômetro. A Figura mostra um sistema que pode ser usado para medir a sua aceleração. Um observador que caminha sobre a plataforma mede o ângulo que o fio que sustenta a bola leve forma com o plano vertical. Não há atrito em nenhum ponto.

a) Como se relaciona com a aceleração do sistema?

b) Se e , qual é o ângulo ?

c) Se você pode variar e , qual é o maior ângulo a ser atingido? Explique como você deve ajustar e para isso.

Passo 1

Opa, bora resolver esse problema! O enunciado nos dá o seguinte sisteminha:

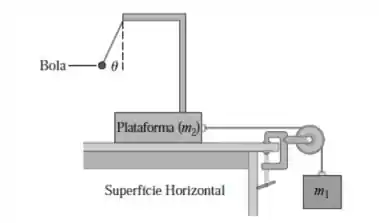
Esse sisteminha é usado para medir a sua aceleração a partir do ângulo . A parada aqui é descobrir como ele acha de . Vamos ao diagrama de forças para a bola:

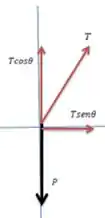
Na vertical, onde não temos movimento, temos que:

Na horizontal, onde temos movimento, temos pela segunda lei de newton que

E dividindo uma equação pela outra teremos uma relação entre o ângulo e a aceleração:

Assim teremos:

Passo 2

b) Ele nos deu os dados das massas do sistema para acharmos . O diagrama de forças para a massa é:

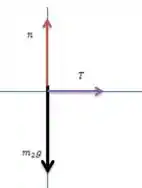
Na vertical temos:

E na horizontal, pela segunda lei de newton:

E para a outra massa o diagrama fica:

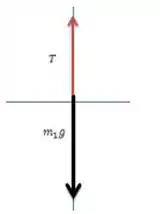
E como essa massa está se movimentando para baixo, a segunda lei dá:

Agora substituindo a tensão encontrada do diagrama de forças da massa nessa equaç��o aqui de cima temos:

Mas daí você se pergunta: onde está o a relação do ângulo nessa história toda? Dá uma espiadela no resultado lá do passo anterior: ! Daqui, se substituirmos ali em cima, vamos ter uma relação entre as massas e o ângulo! Bora fazer?

Passo 3

c) Cara, achamos no passo anterior que:

Daí tiramos que depende de e . Vamos variar essas massas para achar o maior ângulo possível. Temos dois casos possíveis extremos:

- Caso 1: se a massa for muito maior que . Nesse caso, nosso numerador fica muito pequeno e nosso denominador muito grande, o que faz tender a zerar.

Como , não teremos o ângulo máximo nesse caso. E isso vale também se for muito pequeno.

- Caso 2: se for muito maior que . (ou se for muito pequena). Nesse caso, a divisão tende a 1. Como , nosso ângulo máximo é .

Então temos que:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A fig.5-53 mostra um homem sentado em uma cadeira presa a uma corda de massa desprezível que passa por uma roldana de massa e atrito desprezível e desce de volta às mãos do homem. A massa total do hom

Na Fig. 5-64, uma força F → de módulo 12N é aplicada a uma caixa de massa m 2 = 1,0k g . A força é dirigida para cima paralelamente a um plano inclinado de ângulo θ = 37 ° . A caixa está ligada por um

Uma carga de tijolos com 15,0k g é suspensa pela extremidade de uma corda que passa sobre uma pequena polia sem atrito. Um contrapeso de 28,0k g está preso na outra extremidade da corda, conforme most

Dois pesos de 25 N estão suspensos nas extremidades opostas de uma corda que passa sobre uma polia leve e sem atrito. O centro da polia está ligado a uma corrente presa ao teto. a) Qual a tensão na co

Na Figura 5.41 , cada bloco suspenso possui peso p . As polias não possuem atrito e as cordas possuem peso desprezível. Calcule em cada caso a tensão T na corda em termos do peso p . Para cada caso in