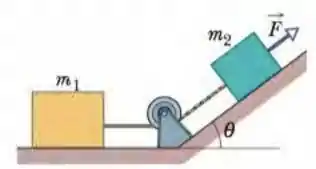
Na Fig. 5-64, uma força F → de módulo 12N é aplicada a uma caixa de massa m 2 = 1,0k g . A força é dirigida para cima paralelamente a um plano inclinado de ângulo θ = 37 ° . A caixa está ligada por uma corda a outra caixa de massa m 1 = 3,0k g situada sobre o piso. O plano inclinado, o piso e a polia não tem atrito e as massas da polia e as massas da polia e da corda são desprezíveis. Qual é a tensão da corda?

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.Problemas Adicionais - Ex. 82

Na Fig. 5-64, uma força de módulo é aplicada a uma caixa de massa . A força é dirigida para cima paralelamente a um plano inclinado de ângulo . A caixa está ligada por uma corda a outra caixa de massa situada sobre o piso. O plano inclinado, o piso e a polia não tem atrito e as massas da polia e as massas da polia e da corda são desprezíveis. Qual é a tensão da corda?

Passo 1

Para determinara tensão na corda, inicialmente vamos determinar a aceleração com que os blocos se deslocam. Para isso, temos que perceber que se considerarmos o sistema com os dois blocos as forças externas que atuam na direção do movimento são uma componente da força peso do bloco e a força . Então, escrevendo a segunda lei de Newton:

Substituindo os valores conhecidos:

Isolando o :

Passo 2

Com a aceleração em mãos, podemos aplicar a segunda lei de Newton para o bloco na direção do movimento. Para tanto, temos que perceber que somente a tensão da corda atua nesta direção e, portanto:

Substituindo os valores:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

41. O livro de física de 1,0k g da FIGURA P7.41 está ligado por um barbante a uma caneca de café de 500g . Dá-se um pequeno empurrão no livro para cima e ele é liberado com uma velocidade de 3,0m / s

40. Uma caixa de 4,0k g , sobre uma rampa sem atrito e inclinada em 35°, está ligada a um peso de 20k g , suspenso, através de um barbante de massa desprezível que passa por uma polia, também sem mass

42. O bonde mostrado na FIGURA P7.42 desce uma colina de 200m de altura. Além dos freios, o bonde pode controlar sua velocidade puxando um contrapeso de 1.800k g que sobe simultaneamente pelo outro la

37. O bloco de 10,2k g da FIGURA P7.37 é mantido em repouso pela corda sem massa que passa por duas polias sem massa e livres de atrito. Determine os valores das tensões de T 1 a T 5 e o módulo da for

33. O coeficiente de atrito estático entre os dois blocos da FIGURA P7.33 vale 0,60 . O coeficiente de atrito cinético entre o bloco inferior e o piso é de 0,20 . A força F → faz com que os dois bloco