Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 5.9 - Ex. 60

A fig.5-53 mostra um homem sentado em uma cadeira presa a uma corda de massa desprezível que passa por uma roldana de massa e atrito desprezível e desce de volta às mãos do homem.

A massa total do homem e da cadeira é 95,0 kg. Qual é o módulo da força com o qual o homem deve puxar a corda para que a cadeira suba

  1. Com velocidade constante
  2. Com uma aceleração para cima de 1,30 m/s²? (Sugestão: um diagrama do por livre pode ajudar bastante).

    3. Se no lado direito a corda estende até o solo e é puxada por uma outra pessoa, qual é o módulo da força com a qual essa pessoa deve puxar a corda para que o homem suba.

  3. Com velocidade contante
  4. Com uma aceleração para cima de 1,30 m/s² ?

    5. Qual é o módulo da força que a polia exerce sobre o teto

  5. No itam a
  6. No item b
  7. No item c
  8. No item d

Passo 1

De inicio você pode pensar o quanto esta questão é grande e complicada,visto que tem vários itens a serem feitos, mas vamos nos acalmar!!!

Como o próprio enunciado nos aconselha, vamos iniciar fazendo um diagrama do corpo livre. Esté método vai nos ajudar a visualizar quais forças estão sendo aplicadas no sistema, e vamos entender o que esta acontecendo em cada situação individualmente. Beleza?!

Passo 2

Vamos então para a construção do nosso diagrama do corpo livre. Temos o peso do homem e a força aplicada para que a cadeira suba.

Precisamos entender que pela terceira lei de Newton, quando o homem puxa a corda a corda puxará o homem com a mesma intensidade, mesma direção e sentido oposto. Vamos agora fazer um somatório de forças existentes no eixo x e no eixo y .

E i x o   x (Não há movimento no eixo x ):

∑ F x = m . a

∑ F x = 0

E i x o   y :

∑ F y = m . a

F h c + F h c - P = m . a

2 F h c - P = m . a

Isolando o F h c , temos

F h c = m . a + P 2

F h c = m . a + m . g 2

Colocando a massa em evidência, temos a seguinte equação

F h c = m . ( a + g ) 2

Agora utilizaremos essa equação para resolver os itens pedidos. ;)

Passo 3

  1. Qual é o módulo da força com o qual o homem deve puxar a corda para que a cadeira suba com velocidade constante.

    2. Em um movimento uniforme, a velocidade é constante. Sendo assim a aceleração é nula.

    F h c = m . ( a + g ) 2

    F h c = m g 2

    Substitutindo os dados e considerando g = 9,8   m / s ² .

    F h c = 95.10 2 = 930 2 = 465,5   N

    Passo 4

  2. Qual é o módulo da força com o qual o homem deve puxar a corda para que a cadeira suba com uma aceleração para cima de 1,30 m/s²?

    3. Substituindo os dados

    F h c = m . ( a + g ) 2

    Note que aqui temos os valores da massa m , da aceleração e da gravidade, então conseguimos encontrar a força

    F h c = 95 . ( 1,3 + 9,8 ) 2 = 1054,5 2 = 527,25   N

    Passo 5

    Para resolver a letra (c) temos que considerar que no lado direito a corda estende até o solo e é puxada por uma outra pessoa. Neste caso teremos apenas uma força aplicada na corda.

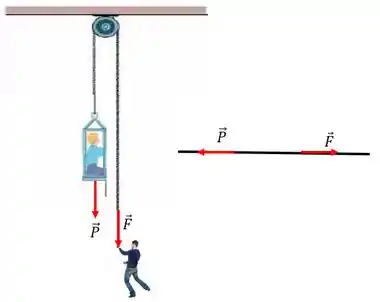
    Para calcular a força na corda podemos fazer o somatório das forças novamente.

    E i x o   y :

    ∑ F y = m . a

    F - P = m . a

    Isolando F

    F = m . a + P

    F = m . a + m g

    F = m . ( a + g )

    Agora sim podemos verificar o que se pede no item c

  3. Qual é o módulo da força com a qual essa pessoa deve puxar a corda para que o homem suba com velocidade contante.

    4. Vamos utilizar a mesma explicação do item a , em um movimento uniforme, a velocidade é constante. Sendo assim a aceleração é nula.

    F = m . ( a + g )

    F = m . g

    F = 95   . 9,8 = 931   N

    Passo 6

  4. Qual é o módulo da força com a qual essa pessoa deve puxar a corda para que o homem suba com uma aceleração para cima de 1,30 m/s²

    5. F = m . ( a + g )

    F = 95 . 1,3 + 9,8 = 1054,5   N

    Passo 7

    Temos agora que calcular a força que a polia exerce sobre o teto. O diagrama de força será.

    Com somatório das forças. Obtemos a seguinte equação:

    F p = 2 F c

    Nos itens a , b , c e d calculamos a força na corda. Sendo assim, basta substiturmos os valores encontrarmos para determinar a força na polia.

  5. F c = 465,5   N

    6. F p = 2   .   465,5  

    F p = 931   N

  6. F c = 527,3   N

    7. F p = 2   .     527,3

    F p = 1054   N

  7. F c = 931   N

    8. F p = 2   .   931

    F p = 1862   N

  8. F c = 1055   N

F p = 2   .   1055

F p = 2110   N

Resposta

a) F h c = 465,5   N

b) F h c = 527,3   N

c) F h c = 931   N

d) F h c = 1055 N

e) F p = 951   N

f) F p = 1054   N

g) F p = 1862   N

h) F p = 2110   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No sistema da figura, m 1 = 20K g ,m 2 = 40K gem 3 = 60K g . Desprezando as massas das polias e dos fios e o atrito, calcule a aceleração do sistema e as tensões nos fios 1,2 e 3.
No sistema da figura ( máquina de Atwood) , mostre que a aceleração a da massa M e a tensão T da orda( desprezando as masss da corda e da polia) são dadas por a = M - m M + m g T = 2 m M M + m g
Um pintor está sobre uma plataforma suspensa de uma polia. Puxando a corda em 3, ele faz a plataforma subir com aceleração g/4. A massa do pintor é de 80 Kg e a da plataforma é de 40 Kg. Calcule as te
Um bloco de massa m 1 = 3,70k g sobre um plano sem atrito inclinado, de ângulo θ = 30,0 ° , está preso por uma corda de massa desprezível, que passa por uma polia de massa e atrito desprezíveis, a um
44. Um pintor de paredes usa o arranjo de uma cadeira e uma polia mostrado na FIGURA P7.44 para se erguer pelo lado externo de uma residência. A massa do pintor é de 70k g , e a da cadeira, 10k g . Co