Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 5.2 - Ex. 19
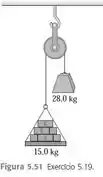
Uma carga de tijolos com é suspensa pela extremidade de uma corda que passa sobre uma pequena polia sem atrito. Um contrapeso de está preso na outra extremidade da corda, conforme mostra a Figura . O sistema é libertado a partir do repouso.
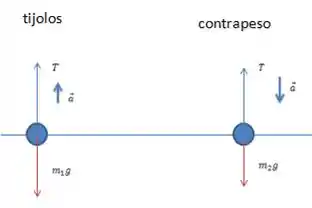
a) Desenhe um diagrama do corpo livre para a carga de tijolos e outro para o contrapeso.
b) Qual é o módulo da aceleração de baixo para cima da carga de tijolos?
c) Qual é a tensão na corda durante o movimento da carga? Como essa tensão é relacionada com a carga? Como essa tensão é relacionada com o contrapeso?
Passo 1
Fala galera! Beleza?! Bora resolver essa questão!
O enunciado nos deu uma carga de tijolos de que está suspensa por uma corda que passa por uma polia, sem atrito. Na outra extremidade da corda, tem um contrapeso de e o sistema é liberado a partir do repouso.
Então, nós precisamos (a) esboçar o diagrama de corpo livre para a carga de tijolos e para o contrapeso, (b) determinar a aceleração da carga de tijolos e (c) a tensão na corda.
Pra isso, vamos usar a segunda lei de Newton (), para definir os valores das nossas forças e da nossa aceleração.
Vamos lá!
Passo 2
a) Vamos entender as forças que estão atuando ali para desenhar o nosso diagrama do corpo livre, que vai, inclusive, nos ajudar a responder o resto da questão.
Nesse sistema estão agindo apenas dois tipos de focas:
- a força peso, aplicada em cada parte (tijolos e contrapeso) é vertical para baixo e é proporcional a massa de cada um;
- a tensão do fio, , que é igual para os dois elementos e ambas apontam verticalmente para cima.
Vamos definir a massa dos tijolos como e a força peso associada é . Já a massa associada ao contrapeso será e sua força peso .
Os diagramas para cada um estão aqui:
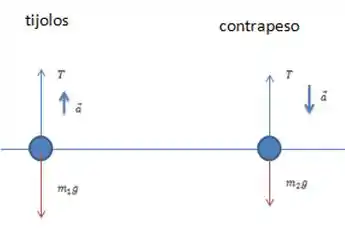
Como a massa do contrapeso é maior que a de tijolos, é nesse sentido que o sistema vai se movimentar, ou seja, sua aceleração é para baixo, Logo, a aceleração dos tijolos será para cima (puxada pelo contrapeso).
Passo 3
b) Para achar a aceleração devemos aplicar a segunda lei de Newton para cada objeto. Vamos calcular nossas forças pesos antes. Para a carga de tijolos:
E para o contrapeso:
Para o contrapeso, a aceleração está para baixo, então vamos considerar para baixo. A segunda lei fica:
Substituindo os dados, temos:
Agora aplicando a segunda lei para os tijolos, temos a aceleração para cima, então vamos considerar para cima
Passo 4
Temos duas equações e duas incógnitas, então podemos achar através do sistema:
Isolando nas duas, temos:
Igualando as equações,
E isolando :
Obtemos a aceleração:
Passo 5
c) Para achar a gente substitui a aceleração que achamos em uma das equações do nosso sisteminha. Podemos escolher:
Vemos que a tensão é maior que o peso da carga e menor que o peso do contrapeso, e isso está de acordo com o sentido da aceleração que nós supomos.
Valeu, galera! Até a próxima! 😉
Resposta
a)
