Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 5.Problemas - Ex. 6
Ache a capacitância equivalente ao sistema infinito de capacitores da figura, entre os pontos e .
Sugestão: Note que a capacitância à direita da linha vertical interrompida equivale a do sistema todo, por ser ele infinito.
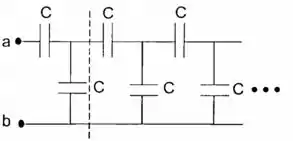
Passo 1
Para facilitar nosso trabalho, vamos separar nosso conjunto de capacitores em duas partes, conforme a figura. Beleza?!
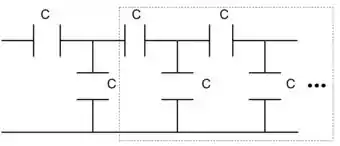
Onde chamaremos a capacitância equivalente do lado direito de . Repare na imagem que ele está em paralelo com o o capacitor do meio. Portanto, podemos achar o capacitor equivalente entre as duas que será .
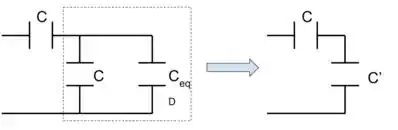
Onde
Passo 2
Na figura podemos perceber que o capacitor está em paralelo com , então a capacitância equivalente de todo o sistema é
Levando em consideração que
Temos
Resolvendo essa equação de 2º grau, temos
Resposta
Exercícios de Livros Relacionados
Verdadeiro ou falso: A capacitância equivalente de dois capacitores em paralelo é sempre maior que o valor das duas capacitâncias. A capacitância equivalente de dois capacitores em série é sempre meno
Um capacitor de 1,00μ F é conectado em paralelo a um capacitor de 2,00μ F e esta combinação é conectada em série com um capacitor de 6,00μ F . Qual é a capacitância equivalente desta combinação?
Um capacitor de placas paralelas tem capacitância C 0 quando não há um dielétrico no espaçamento entre as placas. Este espaçamento é, então, preenchido com um material que tem uma constante dielétrica
Três capacitores têm capacitâncias de 2,00μ F , 4,00μ F e 8,00μ F . Determine a capacitância equivalente se (a) os capacitores estão conectados em paralelo e (b) os capacitores estão conectados em sér
Uma combinação em paralelo de dois capacitores idênticos de 2,00μ F , de placas paralelas (sem dielétrico no espaço entre as placas) é conectada a uma bateria de 100V . A bateria é, então, removida e