Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 3.Problemas - Ex. 16
Um cilindro circular muito longo, de raio , está uniformemente carregado, com densidade volumétrica de carga .
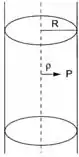
- Por argumentos de simetria (explicando-os), obtenha a direção e o sentido do campo num ponto à distância do eixo do cilindro e sua dependência das cordenadas cilíndricas ().
- Calcule num ponto interno ao cilindro ()
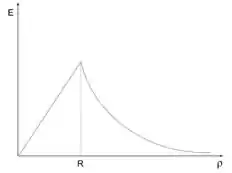
- Esboce o gráfico de em função de .
Passo 1
Se liga! Estamos tratando de uma superfície cinlíndrica! As linhas de campo apontam do eixo que corta o centro dos planos para fora na direção radial. Como o clilindro é muito longo, desconsideramos os efeitos das tampas. Sendo assim, o campo em indepedende de e .
Passo 2
Para o item (b) devemos lembrar que estamos tratando de uma superfície cinlindrica! Então, nada melhor que usar a lei de Gauss. Vamos traçar uma gaussiana cilíndrica de raio .
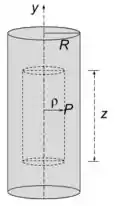
Como o cilindro é muito longo desconsideramos os efeitos de borda.
Que tal aplicar a lei de Gauss?!
onde a área desejada é correspondente a lateral do cilindro
e é a carga dentro da gaussiana
Substituindo e podemos escrever o campo como
Como ele aponta para fora na direção radial, temos
Passo 3
Para esboçar o gráfico pedíamos, precisamo conhecer como é o campo elétrico para . Podemos novamente desenhar uma superfície gaussiana. Se liga no desenho.
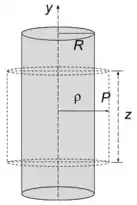
Aplicando novamente a lei de Gauss, temos
Agora temos que prestar atenção que a área será a da superfície gaussiana
mas a carga é a que está contida no cilindro original de raio e altura
Aplicando essas informações encontramos
Passo 4
Só precisamos montar o gráfico do campo em função de .Podemos ver que dentro do cilindro o campo cresce linearmente com .
Já fora, o campo decresce com o inverso de .
Assim podemos montar o gráfico.
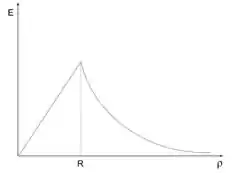
Resposta
