Enunciado
Física - Young and Freedman - Vol 2- Ed: 12º - Capítulo 20.Problemas - Ex. 60
a)Faça um gráfico do ciclo de Carnot, indicando a entropia no eixo horizontal e a temperatura em Kelvin no eixo vertical. Trata-se de um diagrama temperatura -entropia, ou diagrama . b) Mostre que a área embaixo da curva que representa qualquer processo reversível no diagrama representa o calor absorvido pelo sistema.c) Utilize o diagrama para deduzir a eficiência térmica do ciclo de Carnot.d) Faça m diagrama do ciclo de Stirling descrito no Problema 20.50. Use esse diagrama para relacionar a eficiência do ciclo de Stirling com a eficiência do ciclo de Carnot.
Passo 1
Para um processo isotérmico reversível, .
Para um processo adiabático reversível, e .
O ciclo de Carnot consiste em dois processos isotérmicos reversíveis e dois processos adiabáticos reversíveis.
(Use os resultados para o ciclo Stirling do Problema 20.50.)
Passo 2
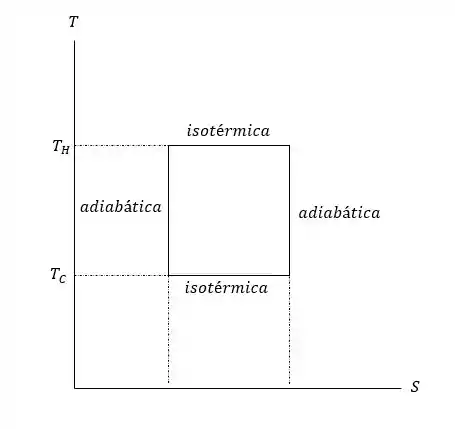
- O gráfico fica da seguinte forma:
- Para um processo reversível,
- é a área sob o retângulo delimitada pela parte horizontal do retângulo em e pelas verticais. é a área delimitada pela parte horizontal do retângulo em e pelas verticais. O trabalho total é então , a área delimitada pelo retângulo que representa o processo. A proporção das áreas é a proporção dos comprimentos dos lados verticais dos respectivos retângulos, e a eficiência é
- Conforme explicado no Problema 20.50, a substância que medeia a troca de calor durante a expansão isocórica e a compactação não sai do sistema e o diagrama é o mesmo da parte (a). Como encontrado nesse problema, a eficiência ideal é a mesma que para um motor de ciclo de Carnot.
Passo 3
e então,
e
qual é a área sob a curva no plano .
Passo 4
Passo 5
A derivação do usando o conceito de entropia é muito mais simples que a derivação na Seção 20.6, mas produz o mesmo resultado.
Resposta
-
- Mostrado no Passo3;