Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 20.Problemas Adicionais - Ex. 62
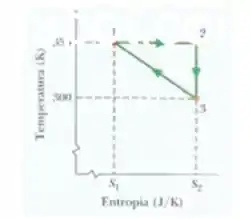
Suponha que de um gás diatômico ideal sejam submetidos reversivelmente ao ciclo mostrado no diagrama na figura abaixo, onde e . As moléculas não giram nem oscilam. Qual é a energia transferida na forma de calor
na trajetória
na trajetória , e
no ciclo completo?
Qual é o trabalho para o processo isotérmico?
O volume é .
Qual é o volume
no estado , e
no estado ?
Qual é a variação
na trajetória
na trajetória e
no ciclo completo? (Sugestão:o item pode ser r-esolvido em uma ou duas linhas de cálculos, usando os resultados da seção ou em uma página de cálculos usando os resultados da seção .)
Qual é o trabalho para o processo adiabático?
Passo 1
Olá pessoal, tudo bem? Vamos treinar um pouco de segunda lei da termodinâmica?
Bom, sabendo que a área de baixo da curva de cada processo fornece a quantidade de calor inserida, no processo a área abaixo da curva (área de um retângulo) é:
-
Passo 2
O calor absorvido em um processo à entropia constante, ou seja é zero! Mas como?
Assim ó:
Show!
Passo 3
O calor do ciclo completo vai ser a área dentro do ciclo. Como a área do ciclo fechado é um triângulo, fica tranquilo de calcular:
Passo 4
O trabalho em um processo isotérmico vai ser, pela primeira lei:
Igual ao calor! E o calor acabamos de encontrar no Passo :
Passo 5
Aqui temos de lembrar que num processo isotérmico o trabalho é
E entre no processo , , o trabalho acabamos de determinar no passo anterior, o número de mols é e a temperatura é :
Passo 6
O volume no estado , temos no processo : , então entre esses estados temos a seguinte relação:
Nesse caso temos (isso porque as moléculas não giram nem oscilam), , e . Agora é só substituir:
Passo 7
A variação da energia interna no processo , que é um processo isotérmico, é zero, pois a avariação de energa interna depende da variação da temperatura, e como esse último é zero, então .
Passo 8
O processo é adiabático, então não há troca de calor com o meio, assim, pela primeira lei da termodinâmica, a variação de energia interna vai ser igual a:
Eu segui direitinho a sugestão! =D
Vamos pras últimas? Juro que está quase no fim!
Passo 9
Para o ciclo completo, devemos lembrar de uma coisa: a energia interna é função de estado e sendo assim, em um ciclo completo, o estado final é igual ao inicial e a variação da energia interna é zero!
Passo 10
Por fim, o problema pede o trabalho para o processo adiabático. Lembrando da primeira lei da termodinâmica, sabemos que em um processo adiabático , daí a primeira lei fica assim:
Mas acabamos de determinar a variação de energia interna justamente para esse processo adiabático (dá uma espiada no Passo )!
Agora é só substituir: