Um fluido é submetido a um ciclo reversível. Se o ciclo é representado por um diagrama no plano , onde é a entropia do fluido, (a) Mostre que o trabalho associado ao ciclo é dado por , a área orientada poe ele compreendida. (b) Represente um ciclo de Carnot para um gás ideal no plano . Verifique o resultado da parte (a) neste caso. (c) Calcule o rendimento do ciclo de Carnot da parte (b) diretamente a partir do diagrama .

(b) Vamos começar relembrando das etapas em um ciclo de Carnot:

E vamos lembrar também da relação entre e :

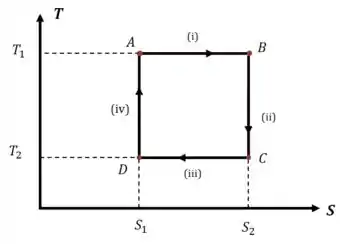
(i) Durante a expansão isotérmica, a temperatura se mantém constante e a entropia aumenta porque o gás recebe calor para expandir. Então temos uma reta horizontal à temperatura .

(ii) Durante a expansão adiabática, , então . Mas a temperatura diminui, então temos uma reta vertical à entropia .

(iii) Durante a compressão isotérmica, a temperatura fica constante e a entropia diminui, porque o gás cede calor ao ser comprimido. Então temos uma reta horizontal à temperatura .

(iv) Durante a compressão adiabática, , então . Mas a temperatura aumenta conforme o gás é comprimido, então temos uma reta vertical à entropia .

Juntando tudo isso, podemos fazer o gráfico no diagrama :

(c) E agora vamos calcular o rendimento do ciclo usando o gráfico que acabamos de desenhar:

O trabalho realizado pelo gás ao longo do ciclo (conforme demonstramos no primeiro passo), segue a seguinte fórmula:

Que é simplesmente a área do quadrado:

E para calcular , temos que considerar apenas os trechos em que o gás absorve calor.

Conforme explicamos no passo anterior, isso só acontece no trecho , que é isotérmico, então:

Então a eficiência é:

Onde é a temperatura da fonte fria e é a temperatura da fonte quente.